题目内容
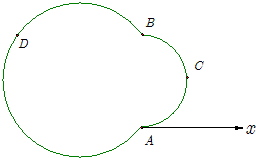 在极坐标系中,极点为A,已知“葫芦”型封闭曲线Ω由圆弧ACB和圆弧BDA组成.已知B(4,
在极坐标系中,极点为A,已知“葫芦”型封闭曲线Ω由圆弧ACB和圆弧BDA组成.已知B(4,| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| 3π |
| 4 |
(1)求圆弧ACB和圆弧BDA的极坐标方程;
(2)求曲线Ω围成的区域面积.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)圆弧ACB是以(2,
)为圆心、2为半径的半圆弧,即可得出圆弧ACB的极坐标方程(0≤θ≤
).圆弧BDA是以(2
,
)为圆心,2
为半径的圆弧,即可得出极坐标方程(
≤θ≤
).
(2)曲线Ω围成的区域面积=
π×22+π(2
)2+
×π×(2
)2-
×(2
)2.
| π |
| 2 |
| π |
| 2 |
| 2 |
| 3π |
| 4 |
| 2 |
| π |
| 2 |
| 5π |
| 4 |
(2)曲线Ω围成的区域面积=
| 1 |
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 2 |
| 2 |
解答:
解:(1)圆弧ACB是以(2,
)为圆心、2为半径的半圆弧,
∴圆弧ACB的极坐标方程为:ρ=4sinθ(0≤θ≤
).
圆弧BDA是以(2
,
)为圆心,2
为半径的圆弧,
其极坐标方程为:ρ=4(sinθ-cosθ)(
≤θ≤
).
(2)曲线Ω围成的区域面积=
π×22+π(2
)2+
×π×(2
)2-
×(2
)2=12π-4.
| π |
| 2 |
∴圆弧ACB的极坐标方程为:ρ=4sinθ(0≤θ≤
| π |
| 2 |
圆弧BDA是以(2
| 2 |
| 3π |
| 4 |
| 2 |
其极坐标方程为:ρ=4(sinθ-cosθ)(
| π |
| 2 |
| 5π |
| 4 |
(2)曲线Ω围成的区域面积=
| 1 |
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 2 |
| 2 |
点评:本题考查了直角坐标方程极坐标方程、圆的面积,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
函数f(x)=lnx+x2-4零点所在的大致区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
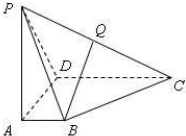 如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=| 1 |
| 2 |
(1)求证:PD⊥AB;
(2)在侧棱PC上是否存在一点Q,使BQ∥平面PAD?证明你的结论.
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m⊥n,m⊥α,n∥β,则α∥β |
| B、若m∥α,n∥β,α∥β则m∥n |
| C、若m∥n,m∥α,n∥β,则α∥β |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
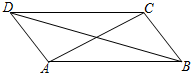 如图,平行四边形ABCD中,向量
如图,平行四边形ABCD中,向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
