题目内容
已知数列{an}的前n项和为Sn,已知a1=2,且nSn+1-(n+1)Sn=n(n+1)(n∈N+),则过A(n,an)和B(n+2,an+2)的直线的一个方向向量的坐标可以是( )
| A、(2,-4) | ||||
| B、(-1,-1) | ||||
C、(-
| ||||
D、(1,-
|
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得{
}是首项为2,公差为1的等差数列,从而Sn=n2+n,进而an=2n.由此得
=(n+2-n,an+2-an)=(2,4),从而能求出结果.
| Sn |
| n |
| AB |
解答:
解:∵数列{an}的前n项和为Sn,
a1=2,且nSn+1-(n+1)Sn=n(n+1)(n∈N+),
∴
-
=1,又
=2,
∴{
}是首项为2,公差为1的等差数列,
∴
=2+(n-1)=n+1,
∴Sn=n2+n,
∴a1=S1=1+1=2,
当n≥2时,an=Sn-Sn-1=(n2+n)-(n-1)2-(n-1)=2n,
n=1时,上式成立,故an=2n.
∵A(n,an)和B(n+2,an+2),
∴
=(n+2-n,an+2-an)=(2,4),
∴过A(n,an)和B(n+2,an+2)的直线的一个方向向量的坐标可以是(-
,-
).
故选:C.
a1=2,且nSn+1-(n+1)Sn=n(n+1)(n∈N+),
∴
| Sn+1 |
| n+1 |
| Sn |
| n |
| S1 |
| 1 |
∴{
| Sn |
| n |
∴
| Sn |
| n |
∴Sn=n2+n,
∴a1=S1=1+1=2,
当n≥2时,an=Sn-Sn-1=(n2+n)-(n-1)2-(n-1)=2n,
n=1时,上式成立,故an=2n.
∵A(n,an)和B(n+2,an+2),
∴
| AB |
∴过A(n,an)和B(n+2,an+2)的直线的一个方向向量的坐标可以是(-
| 1 |
| 4 |
| 1 |
| 2 |
故选:C.
点评:本题考查方向向量的坐标的判断与求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知F是椭圆
+
=1(a>b>0)的右焦点,过点F作斜率为2的直线l使它与圆x2+y2=b2相切,则椭圆离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
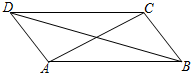 如图,平行四边形ABCD中,向量
如图,平行四边形ABCD中,向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
设关于x的不等式x2-2x-(a2-2a)<0的解集为A,若2∈A,则实数a的取值范围为( )
| A、(0,2) |
| B、(-∞,0) |
| C、(2,+∞) |
| D、(-∞,0)∪(2,+∞) |
sin(2π-α)cos(
| ||||
tan(α-3π)sin(
|
| A、-cosα | B、cosα |
| C、sinα | D、-sinα |