题目内容
若关于x的不等式|x+1|＜6-|x-m|的解集为∅，则实数m的取值范围是 ．
考点：绝对值不等式
专题：不等式的解法及应用
分析：利用绝对值的几何意义求得|x+1|+|x-m|的最小值为|m+1|，结合题意可得|m+1|≥6，由此求得实数m的取值范围．
解答：
解：由于关于x的不等式|x+1|+|x-m|＜6的解集为∅，
而|x+1|+|x-m|表示数轴上的x对应点到-1、m对应点的距离之和，它的最小值为|m+1|，
故有|m+1|≥6，∴m+1≥6，或bm+1≤-6，求得m≤-7，或m≥5，
故答案为：（-∞，-7]∪[5，+∞）．
而|x+1|+|x-m|表示数轴上的x对应点到-1、m对应点的距离之和，它的最小值为|m+1|，
故有|m+1|≥6，∴m+1≥6，或bm+1≤-6，求得m≤-7，或m≥5，
故答案为：（-∞，-7]∪[5，+∞）．
点评：本题主要考查绝对值的意义，绝对值不等式的解法，体现了等价转化的数学思想，属于基础题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知F是椭圆
+
=1（a＞b＞0）的右焦点，过点F作斜率为2的直线l使它与圆x2+y2=b2相切，则椭圆离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
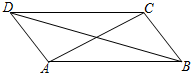如图，平行四边形ABCD中，向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
设关于x的不等式x2-2x-（a2-2a）＜0的解集为A，若2∈A，则实数a的取值范围为（ ）
| A、（0，2） |
| B、（-∞，0） |
| C、（2，+∞） |
| D、（-∞，0）∪（2，+∞） |