题目内容
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:构造函f(x)=ln(x+1)-
,判断其在各区间端点的函数值是否相反,根据根的存在性定理,端点函数值相反的是函数零点所在区间,即方程的根所在区间.
| 2 |
| x |
解答:
解:由题意设函数f(x)=ln(x+1)-
,
并且f(0)→-∞,f(1)=ln2-2<0;f(2)=ln3-1>0,f(e)=ln(e+1)-
>0,f(3)=ln4-
>0,f(4)=ln5-
>0,
根据方程根的存在性定理可知,方程ln(x+1)-
=0,(x>0)的根存在的大致区间是(1,2);
故选B.
| 2 |
| x |
并且f(0)→-∞,f(1)=ln2-2<0;f(2)=ln3-1>0,f(e)=ln(e+1)-
| 2 |
| e |
| 2 |
| 3 |
| 1 |
| 2 |
根据方程根的存在性定理可知,方程ln(x+1)-
| 2 |
| x |
故选B.
点评:本题考查了方程根的存在性的判断;根据方程根的存在性定理,连续函数在某个区间存在零点的条件是函数在区间端点处的函数值异号.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m⊥n,m⊥α,n∥β,则α∥β |
| B、若m∥α,n∥β,α∥β则m∥n |
| C、若m∥n,m∥α,n∥β,则α∥β |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
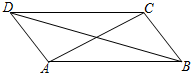 如图,平行四边形ABCD中,向量
如图,平行四边形ABCD中,向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
若条件p:|x+1|>2,条件q:x>a且¬p是¬q的充分不必要条件,则a取值范围是( )
| A、a≥1 | B、a≤1 |
| C、a≥-3 | D、a≤-3 |
 如图,在边长为2的正三角形ABC中,点P满足
如图,在边长为2的正三角形ABC中,点P满足