题目内容
7．已知数列{an}的前n项和Sn=n2+n，则a1+a3+a5+a7+a9=（ ）| A． | 50 | B． | 45 | C． | 90 | D． | 80 |
分析 由Sn=n2+n，数列{an}以2为首项，以2为公差的等差等差数列，根据等差数列的性质，即可求得答案．
解答 解：数列{an}的前n项和为Sn=n2+n，
可得a1=2，
当n≥2时，an=Sn-Sn-1=n2+n-（n-1）2-（n-1）=2n．
n=1时满足通项公式，
数列{an}以2为首项，以2为公差的等差等差数列，
a1+a3+a5+a7+a9=2+6+10+14+18=50，
故选：A．
点评 本题考查等差数列的通项公式，考查等差数列的性质，考查计算能力，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
17．下列函数中，在其定义域内是增函数而且又是奇函数的是（ ）
| A． | $y=x+\frac{1}{x}$ | B． | y=2x-2-x | C． | y=log2|x| | D． | y=2x+2-x |
15．下列命题中错误的是（ ）
| A． | 如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥γ | |
| B． | 如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β | |
| C． | 如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β | |
| D． | 如果平面α⊥平面β，α∩β=l，过α内任意一点作l的垂线m，则m⊥β |
2．数列{an}满足a1=2，an=$\frac{{a}_{n+1}-1}{{a}_{n+1}+1}$，其前n项的积为Tn，则T2016的值为（ ）
| A． | -3 | B． | 1 | C． | 2 | D． | $\frac{1}{3}$ |
12．“z1与z2互为共轭复数”是“z1z2∈R”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要条件 | D． | 既不充分也不必要 |
19．设集合M={1，2}，N={a2}，则“a=1”是“N是M的子集”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
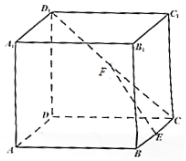如图，在正方体ABCD-A1B1C1D1中，E、F分别是线段BC、CD1的中点．