题目内容
15.下列命题中错误的是( )| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,α∩β=l,过α内任意一点作l的垂线m,则m⊥β |
分析 根据空间中直线与直线,直线与平面位置关系及几何特征,逐一分析给定四个结论的真假,可得答案.
解答 解:如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ,故A正确;
如果平面α⊥平面β,那么平面α内一定存在平行于交线的直线平行于平面β,故B正确;
如果平面α内存在直线垂直于平面β,则平面α⊥平面β,故如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β,故C正确;
如果平面α⊥平面β,过α内任意一点作交线的垂线,如果点取在交线上则垂线垂直于β,错误.故D错误;
故选:D.
点评 本题以命题的真假判断与应用为载体,考查了空间直线与直线,直线与平面位置关系及几何特征,难度中档.

练习册系列答案
相关题目
5.已知f(x)为定义在(0,+∞)上的可导函数,且f(x)>xf'(x),则不等式${x^2}f(\frac{1}{x})-f(x)<0$的解集为( )
| A. | (0,4) | B. | (0,3) | C. | (0,2) | D. | (0,1) |
6.sin(-$\frac{10π}{3}$)的值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
3.已知函数f(x)=ax3+c,且f′(1)=6,函数在[1,2]上的最大值为20,则c的值为( )
| A. | 1 | B. | 4 | C. | -1 | D. | 0 |
20.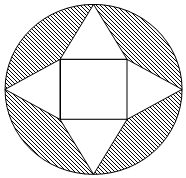 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{6}$ |
7.已知数列{an}的前n项和Sn=n2+n,则a1+a3+a5+a7+a9=( )
| A. | 50 | B. | 45 | C. | 90 | D. | 80 |
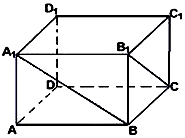 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,