题目内容
12.“z1与z2互为共轭复数”是“z1z2∈R”的( )条件.| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
分析 设z1=a+bi(a,b∈R),z1与z2互为共轭复数,z2=a-bi,可得z1z2∈R.反之不成立,举例即可说明.
解答 解:设z1=a+bi(a,b∈R),z1与z2互为共轭复数,则z2=a-bi,
则z1z2=a2+b2∈R.
反之不成立:例如取z1=i,z2=2i,则z1z2=-2∈R.但是z1与z2不互为共轭复数.
∴“z1与z2互为共轭复数”是“z1z2∈R”的充分不必要条件.
故选:A.
点评 本题考查了复数的有关知识、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
3.已知函数f(x)=ax3+c,且f′(1)=6,函数在[1,2]上的最大值为20,则c的值为( )
| A. | 1 | B. | 4 | C. | -1 | D. | 0 |
20.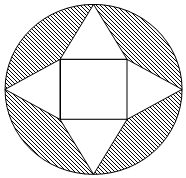 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{6}$ |
7.已知数列{an}的前n项和Sn=n2+n,则a1+a3+a5+a7+a9=( )
| A. | 50 | B. | 45 | C. | 90 | D. | 80 |
1.在△ABC中,角A、B、C所对的边分别为a、b、c,且b(2sinB-sinA)+(2a-b)sinA=2csinC,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
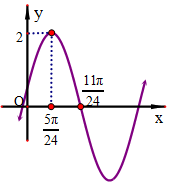 已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.
已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.