Question

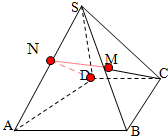
在四棱锥S-ABCD中，AB∥CD，AB=BC=2，CD=SD=1，BC⊥CD，M为SB的中点，DS⊥面SAB．
（1）求证：CM∥面SAD；
（2）求证：CD⊥SD；
（3）求四棱锥S-ABCD的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：空间位置关系与距离

分析：（1）利用平行线中的一条直线与令一条直线垂直，推出另一条直线垂直证明CD⊥SD；
（2）取SA中点N，连接ND，NM，证明NMCD是平行四边形，通过ND∥MC，证明CM∥面SAD；
（3）利用V_S-ABCD：V_S-ABD=S_ABCD：S_△ABD，求出V_S-ABD，即可求四棱锥S-ABCD的体积．

解答： （1）证明：取SA的中点，
∵M为SB的中点，
∴MN∥AB，MN=

1

2

AB，
∵AB=2，CD=1，
∴MN∥CD，MN=DC，
∴四边形MNDC为平行四边形，
∴CM∥ND，ND?面SAD，CM?面SAD；
∴CM∥面SAD


证明：（2）∵DS⊥面SAB，AB?面SAB．
∴DS⊥AB，
∵AB∥DC，
∴DS⊥DC，
解：（3）V_S-ABCD：V_S-ABD=S_ABCD：S_△ABD=3：2，
过D作DH⊥AB，交于H，由题意得，BD=AD=

12+22

=

5

，
在Rt△DSA，Rt△DSB中，SA=SB=

( 5 )2-1

=2．
所以，V_S-ABD=V_D-SAB=

1

3

×S_△ABS×DS=

1

3

×

3

×1=

3

3

，
四棱锥S-ABCD的体积为：

3

2

×

3

3

=

3

2

；

点评：考查直线与直线垂直，直线与平面平行的证明，几何体的体积的求法，考查空间想象能力，计算能力．