题目内容

求函数y=x-
x
值域．
考点：函数的值域
专题：函数的性质及应用
分析：先对根式整体换元（注意求新变量的取值范围），把原问题转化为一个二次函数在闭区间上求值域的问题即可．
解答： 解：设t=
x
，t≥0，
∴y=t2-t=（t-
1
2
）2-
1
4
，
∵t≥0，
∴当t=
1
2
时，函数有最小值，即y=-
1
4
，无最大值，
故函数的值域为[-
1
4
，+∞）
点评：本题主要考查用换元法求值域以及二次函数在闭区间上求值域问题．换元法求值域适合于函数解析式中带根式且根式内外均为一次形式的题目，属于基础题
练习册系列答案
相关题目
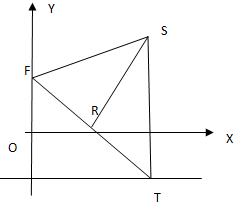在平面直角坐标系中，O为坐标原点，点 F，T，R，S满足
OF
=(0，1)，
OT
=（t，-1），
FR
=
RT
，
SR
⊥
FT
，
ST
∥
OF

（1）当t变化时，求点S的轨迹方程C；
（2）过动点T（t≠0）向曲线C作两条切线，切点分别为A，B，求证：kTA•kTB为定值，并求出这个定值；
（3）在（2）的条件下，探索直线AB是否过定点，若过定点，求出该点；若不过定点，请说明理由．
设抛物线M：y2=4x的焦点F是椭圆N：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点．若M与N的公共弦AB恰好过F，则椭圆的长轴长为
 
．
以坐标原点为极点，横轴的正半轴为极轴的极坐标系下，有曲线C：ρ=4cosθ，过极点的直线θ=φ（φ∈R且φ是参数）交曲线C于两点0，A，令OA的中点为M．
（1）求点M在此极坐标下的轨迹方程（极坐标形式）．
（2）当φ=
5π
3
时，求M点的直角坐标．
已知函数f（x）=x3-ax2-2在（2，+∞）上是增函数，则a的取值范围是
 
．
已知二次函数y=x2-2x-3的图象与x轴交于两点A，B（xA＜xB），与y轴交于点C，△ABC的外接圆的圆心为M（1，-1），斜率为3的直线l与⊙M交于不同两点E，F，且满足ME⊥MF．
（1）求点A，B，C的坐标及⊙M的半径R的值；
（2）求直线l的方程；
（3）设P是直线l上的动点，且点A，C在l的同侧，求||PA|-|PC||的最大值及取得最大值时点P的坐标．
在四棱锥S-ABCD中，AB∥CD，AB=BC=2，CD=SD=1，BC⊥CD，M为SB的中点，DS⊥面SAB．
（1）求证：CM∥面SAD；
（2）求证：CD⊥SD；
（3）求四棱锥S-ABCD的体积．
已知点A（2，3），B（5，4），C（10，8），若
AP
=
AB
+λ
AC
（λ∈R），求当λ为何值时：
（1）点P在直线y=x上？
（2）点P在第二象限内？
设椭圆
x2
4
+
y2
3
=1的左右焦点分别为F1，F2，过F1的直线l与椭圆相交于A、B两点，则|AF2|+|BF2|的最大值为（　　）
A、5B、3C、4D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网