题目内容
对?n∈N*,13+23+33+…+(n-1)3<n2,n2×S<13+23+33+…+n3恒成立,S∈N*,则S= .
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:依题意,可得n2×S<n2+n3,从而有S<1+n,对?n∈N*恒成立,求得(1+n)min=2,结合S∈N*,即可得到答案.
解答:
解:∵?n∈N*,13+23+33+…+(n-1)3<n2,
∴13+23+33+…+n3<n2+n3,
∵n2×S<13+23+33+…+n3恒成立,
∴n2×S<n2+n3,
∴S<1+n,对?n∈N*恒成立,
∴S<(1+n)min=2,又S∈N*,
∴S=1.
故答案为:1.
∴13+23+33+…+n3<n2+n3,
∵n2×S<13+23+33+…+n3恒成立,
∴n2×S<n2+n3,
∴S<1+n,对?n∈N*恒成立,
∴S<(1+n)min=2,又S∈N*,
∴S=1.
故答案为:1.
点评:本题考查数列递推关系式的理解与应用,分析得到n2×S<n2+n3是关键,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
已知M (0,-2),N (0,4),则以MN为斜边的直角三角形直角顶点P的轨迹方程是( )
| A、x2+y2=4,(y≠±2) |
| B、x2+y2=9 |
| C、x2+(y-1)2=9,(y≠-2且y≠4) |
| D、x2+(y-1)2=9 |
若命题P(n)对n=3成立,且由P(k)成立可以推证P(k+2)也成立,则一定有( )
| A、P(n)对所有正整数都成立 |
| B、P(n)对所有正偶数都成立 |
| C、P(n)对所有正奇数都成立 |
| D、P(n)对所有大于等于3的正奇数都成立 |
平面内,若M到定点F1(0,-1)、F2(0,1)的距离之和为4,则M的轨迹方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
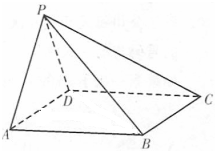 四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.
四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.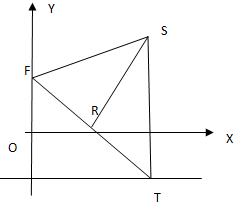 在平面直角坐标系中,O为坐标原点,点 F,T,R,S满足
在平面直角坐标系中,O为坐标原点,点 F,T,R,S满足 在四棱锥S-ABCD中,AB∥CD,AB=BC=2,CD=SD=1,BC⊥CD,M为SB的中点,DS⊥面SAB.
在四棱锥S-ABCD中,AB∥CD,AB=BC=2,CD=SD=1,BC⊥CD,M为SB的中点,DS⊥面SAB.