题目内容
已知函数f(x)=2sin2(
+x)-
cos2x-1,x∈R,若函数h(x)=f(x+α)的图象关于点(-
,0)对称,且α∈(0,π),则α= .
| π |
| 4 |
| 3 |
| π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:利用两角和差的正弦公式、二倍角公式化简函数的解析式为f(x)=2sin(2x-
),可得函数h(x)=2sin(2x+2α-
),再由 h(-
)=0 可得2t-
=0或π,由此解得t的值.
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
解答:
解:∵函数f(x)=2sin2(
+x)-
cos2x-1
=2•
-
cos2x-1
=1+sin2x-
cos2x-1
=2(
sin2x-
sin2x)
=2sin(2x-
),
∴函数h(x)=f(x+α)=2sin(2x+2α-
),且它的图象关于点(-
,0)对称,
∴h(-
)=0,即 2sin(2α-π)=0,
∵α∈(0,π),
∴2α-π=0 解得α=
.
故答案为:
.
| π |
| 4 |
| 3 |
=2•
1-cos(
| ||
| 2 |
| 3 |
=1+sin2x-
| 3 |
=2(
| 1 |
| 2 |
| ||
| 2 |
=2sin(2x-
| π |
| 3 |
∴函数h(x)=f(x+α)=2sin(2x+2α-
| π |
| 3 |
| π |
| 3 |
∴h(-
| π |
| 3 |
∵α∈(0,π),
∴2α-π=0 解得α=
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:本题主要考查两角和差的正弦公式、二倍角公式的应用,正弦函数的对称性,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
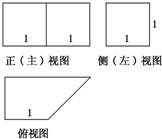
一个几何体的三视图如图所示,则该几何体的表面积为( )

A、6+
| ||
B、7+
| ||
C、8+
| ||
D、7+2
|
已知i是虚数单位,复数z满足:(1-2i)z=(1+i)2,则z的值是( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
 一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是
一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是