题目内容

函数f（x）=log
1
2
（2x-x2）的定义域是
 
．
考点：对数函数的定义域
专题：函数的性质及应用
分析：函数f（x）=log
1
2
（2x-x2）的定义域满足2x-x2＞0，由此能求出结果．
解答： 解：函数f（x）=log
1
2
（2x-x2）的定义域满足：
2x-x2＞0，即x2-2x＜0，
解得0＜x＜2，
故答案为：（0，2）．
点评：本题考查对数函数的定义域的求法，解题时要认真审题，注意对数性质的合理运用．
练习册系列答案
相关题目
条件p：不等式log2（x-1）＜1的解；条件q：不等式x2-2x-3＜0的解，则p是q的
 
．
已知f（x）=sin（x+
π
2
），g（x）=cos（x-
π
2
），则下列结论中正确的序号是
 

（1）函数y=f（x）•g（x）的最小正周期为π．
（2）函数y=f（x）•g（x）的最大值为
1
2
．
（3）函数y=f（x）•g（x）的图象关于点（
π
4
，0）成中心对称      
（4）将函数f（x）的图象向右平移
π
2
个单位后得到函数g（x）的图象．
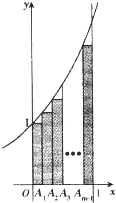如图．A1，A2，…Am-1（m≥2）将区间[0，l]m等分，直线x=0，x=1，y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2．在Ω1中任取一点，则该点取自Ω2的概率等于
 
．
当x∈（0，1）时，不等式x2＜loga（x+1）恒成立，则实数a的范围为
 
．
已知函数f（x）=2sin2（
π
4
+x）-
3
cos2x-1，x∈R，若函数h（x）=f（x+α）的图象关于点（-
π
3
，0）对称，且α∈（0，π），则α=
 
．
为了普及环保知识，增强环保意识，某高中随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为m，众数为n，平均值为
.
x
，则这三个数的大小关系为
 
＜
 
＜
 
．
已知集合M={1，z（1+i）}，i为虚数单位，N={3，4}，若M∪N={1，2，3，4}，则复数z在复平面上所对应的点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
下列有关命题的说法正确的是（　　）
A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
B、“m=1”是“直线x-my=0和直线x+my=0互相垂直”的充要条件
C、命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0”
D、命题“已知x，y为一个三角形的两内角，若x=y，则sinx=siny”的逆命题为真命题

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网