题目内容
已知i是虚数单位,复数z满足:(1-2i)z=(1+i)2,则z的值是( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:把等式两边同时乘以
,然后直接由复数的除法运算化简求值.
| 1 |
| 1-2i |
解答:
解:由(1-2i)z=(1+i)2,
得z=
=
=
=-
+
i.
故选:A.
得z=
| (1+i)2 |
| 1-2i |
| 2i(1+2i) |
| (1-2i)(1+2i) |
| -4+2i |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
故选:A.
点评:本题考查了复数代数形式的除法运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
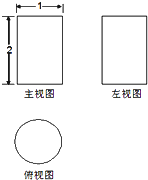 一个空间几何体的主视图和左视图都是矩形,俯视图是一个圆,尺寸如图,那么这个几何体的外接球的体积为( )
一个空间几何体的主视图和左视图都是矩形,俯视图是一个圆,尺寸如图,那么这个几何体的外接球的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某空间几何体的三视图如图所示,则该几何体的表面积为( )


A、12+4
| ||
B、18+8
| ||
| C、28 | ||
D、20+8
|
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“m=1”是“直线x-my=0和直线x+my=0互相垂直”的充要条件 |
| C、命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” |
| D、命题“已知x,y为一个三角形的两内角,若x=y,则sinx=siny”的逆命题为真命题 |
我们把离心率之差的绝对值小于
的两条双曲线称为“相近双曲线”.已知双曲线C:
-
=1,则下列双曲线中与C是“相近双曲线”的为( )
| 1 |
| 2 |
| x2 |
| 4 |
| y2 |
| 12 |
| A、x2-y2=1 | ||||
B、x2-
| ||||
| C、y2-2x2=1 | ||||
D、
|
已知双曲线C1:
-
=1(a>0,b>0)的离心率为
,一条渐近线为l,抛物线C2:y2=4x的焦点为F,点P为直线l与抛物线C2异于原点的交点,则|PF|=( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
三棱锥P-ABC中,PA、PB、PC两两垂直且PA=2
,PB=4,PC=2
,如果三棱锥的四个顶点都在同一球面上,那么这个球的体积等于( )
| 2 |
| 3 |
| A、36π | B、72π |
| C、144π | D、288π |