题目内容
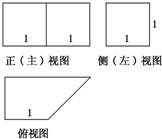
一个几何体的三视图如图所示,则该几何体的表面积为( )

A、6+
| ||
B、7+
| ||
C、8+
| ||
D、7+2
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是直四棱柱,根据三视图判断直四棱柱的高及底面梯形的底边长、高,再求出底面梯形的斜腰长,把数据代入棱柱的表面积公式计算.
解答:
解:由三视图知:几何体是直四棱柱,且直四棱柱的侧棱长为1,
其底面为直角梯形,梯形的上底为1,下底为2,直角腰为1,另一腰长为
=
,
∴其表面积S=2×
×1+(1+2+1+
)×1=3+4+
=7+
.
故选:B.
其底面为直角梯形,梯形的上底为1,下底为2,直角腰为1,另一腰长为
| 1+1 |
| 2 |
∴其表面积S=2×
| 1+2 |
| 2 |
| 2 |
| 2 |
| 2 |
故选:B.
点评:本题考查了由三视图求几何体的表面积,判断几何体的形状及数据所对应的几何量是解答此类问题的关键.

练习册系列答案
相关题目
执行如图所示的程序框图,输出结果S=( )


| A、1006 | B、1007 |
| C、1008 | D、1009 |
已知集合M={1,z(1+i)},i为虚数单位,N={3,4},若M∪N={1,2,3,4},则复数z在复平面上所对应的点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
复数
=( )
| 2i |
| 2-i |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
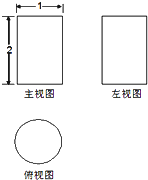 一个空间几何体的主视图和左视图都是矩形,俯视图是一个圆,尺寸如图,那么这个几何体的外接球的体积为( )
一个空间几何体的主视图和左视图都是矩形,俯视图是一个圆,尺寸如图,那么这个几何体的外接球的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某空间几何体的三视图如图所示,则该几何体的表面积为( )


A、12+4
| ||
B、18+8
| ||
| C、28 | ||
D、20+8
|
三棱锥P-ABC中,PA、PB、PC两两垂直且PA=2
,PB=4,PC=2
,如果三棱锥的四个顶点都在同一球面上,那么这个球的体积等于( )
| 2 |
| 3 |
| A、36π | B、72π |
| C、144π | D、288π |
