题目内容
已知函数f(x)满足:f(1)=
,4f(x)f(y)=f(x+y)+f(x-y),则f(2015)= .
| 1 |
| 4 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:运用赋值法,令y=1,根据条件得到f(x)=f(x+1)+f(x-1),将x换为x+1,再把x换为x+1,得到f(x+3)=-f(x),把x换为x+3,得到f(x+6)=f(x),从而f(x)的周期为6,f(2015)=f(5);根据条件再令x=y=0,求出f(0),令x=y=1,求出f(2),令x=2,y=1,求出f(3),令x=y=2,求出f(4),令x=4,y=1求出f(5)即可.
解答:
解:令x=y=0,则4f2(0)=f(0)+f(0),
即f(0)=0或f(0)=
,
若f(0)=0,则令y=0,有4f(x)f(0)=2f(x),
即f(x)=0,这与f(1)>0矛盾,
∴f(0)=
,
∵f(1)=
,
令x=y=1,则4f2(1)=f(2)+f(0),
∴f(2)=4×
-
=-
,
令x=2,y=1,则4f(2)f(1)=f(3)+f(1),
∴f(3)=4×(-
)×
-
=-
,
令x=y=2,则4f2(2)=f(4)+f(0),
∴f(4)=4×
-
=-
,
令x=4,y=1,则4f(4)f(1)=f(5)+f(3),
∴f(5)=4×(-
)×
-(-
)=
,
∵f(1)=
,4f(x)f(y)=f(x+y)+f(x-y),
令y=1,则4f(x)f(1)=f(x+1)+f(x-1)即f(x)=f(x+1)+f(x-1),
∴f(x+1)=f(x+2)+f(x),即f(x+1)=f(x+2)+f(x+1)+f(x-1),
∴f(x+2)=-f(x-1),即f(x+3)=-f(x),
∴f(x+6)=-f(x+3)=f(x),
∴函数f(x)是最小正周期为6的函数,
∴f(2015)=f(6×335+5)=f(5)=
,
故答案为:
.
即f(0)=0或f(0)=
| 1 |
| 2 |
若f(0)=0,则令y=0,有4f(x)f(0)=2f(x),
即f(x)=0,这与f(1)>0矛盾,
∴f(0)=
| 1 |
| 2 |
∵f(1)=
| 1 |
| 4 |
令x=y=1,则4f2(1)=f(2)+f(0),
∴f(2)=4×
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 4 |
令x=2,y=1,则4f(2)f(1)=f(3)+f(1),
∴f(3)=4×(-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
令x=y=2,则4f2(2)=f(4)+f(0),
∴f(4)=4×
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 4 |
令x=4,y=1,则4f(4)f(1)=f(5)+f(3),
∴f(5)=4×(-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∵f(1)=
| 1 |
| 4 |
令y=1,则4f(x)f(1)=f(x+1)+f(x-1)即f(x)=f(x+1)+f(x-1),
∴f(x+1)=f(x+2)+f(x),即f(x+1)=f(x+2)+f(x+1)+f(x-1),
∴f(x+2)=-f(x-1),即f(x+3)=-f(x),
∴f(x+6)=-f(x+3)=f(x),
∴函数f(x)是最小正周期为6的函数,
∴f(2015)=f(6×335+5)=f(5)=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题主要考查函数的周期性和运用,考查解决抽象函数的常用方法:赋值法,注意充分运用条件,恰当赋值和赋式的运用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
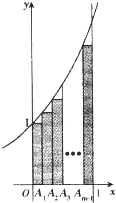 如图.A1,A2,…Am-1(m≥2)将区间[0,l]m等分,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2.在Ω1中任取一点,则该点取自Ω2的概率等于
如图.A1,A2,…Am-1(m≥2)将区间[0,l]m等分,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2.在Ω1中任取一点,则该点取自Ω2的概率等于执行如图所示的程序框图,输出结果S=( )


| A、1006 | B、1007 |
| C、1008 | D、1009 |
某空间几何体的三视图如图所示,则该几何体的表面积为( )


A、12+4
| ||
B、18+8
| ||
| C、28 | ||
D、20+8
|
