题目内容

设等比数列{an}的前n项和为Sn，若a1=1，S6=4S3，则a3=
 
．
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：由已知条件推导出
1-q6
1-q
=4×
1-q3
1-q
，由此利用等比数列的通项公式能求出a3．
解答： 解：∵等比数列{an}的前n项和为Sn，a1=1，S6=4S3，
∴q≠1，且
1-q6
1-q
=4×
1-q3
1-q
，
∴1+q3=4，q3=3，解得q=
33
．
∴a3=q2=
39
．
故答案为：
39
．
点评：本题考查等比数列的前n项和公式的应用，是基础题，解题时要认真审题，要熟练掌握等比数列的基本性质．
练习册系列答案
相关题目
如图，延长⊙O的半径OA到B，使OA=AB，DE是圆的一条切线，E是切点，过点B作DE的垂线，垂足为点C．
求证：∠ACB=
1
3
∠OAC．
已知圆C的圆心是双曲线
y2
12
-
x2
4
=1的上焦点，直线4x-3y-3=0与圆C相交于A，B两点，且|AB|=8，则圆C的方程为
 
．
按如下程序框，最后输出i的结果是
 
已知f（x）=sin（x+
π
2
），g（x）=cos（x-
π
2
），则下列结论中正确的序号是
 

（1）函数y=f（x）•g（x）的最小正周期为π．
（2）函数y=f（x）•g（x）的最大值为
1
2
．
（3）函数y=f（x）•g（x）的图象关于点（
π
4
，0）成中心对称      
（4）将函数f（x）的图象向右平移
π
2
个单位后得到函数g（x）的图象．
已知直线l：y=-
3
（x-1）与圆O：x2+y2=1在第一象限内交于点M，且l与y轴交于点A，则△MOA的面积等于
 
．
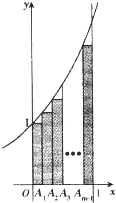如图．A1，A2，…Am-1（m≥2）将区间[0，l]m等分，直线x=0，x=1，y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2．在Ω1中任取一点，则该点取自Ω2的概率等于
 
．
已知函数f（x）=2sin2（
π
4
+x）-
3
cos2x-1，x∈R，若函数h（x）=f（x+α）的图象关于点（-
π
3
，0）对称，且α∈（0，π），则α=
 
．
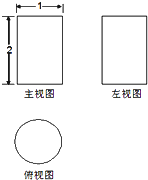一个空间几何体的主视图和左视图都是矩形，俯视图是一个圆，尺寸如图，那么这个几何体的外接球的体积为（　　）
A、
4
2
3
π
B、
8
2
3
π
C、
5
6
π
D、
5
5
6
π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网