题目内容
7．已知直线l的方程为$x-\sqrt{3}y+2=0$，则直线l的倾斜角为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 150° |
分析 设直线l的倾斜角为θ，则tanθ=$\frac{1}{\sqrt{3}}$，即可得出．
解答 解：设直线l的倾斜角为θ，则tanθ=$\frac{1}{\sqrt{3}}$，则θ=30°．
故选：A．
点评 本题考查了直线的斜率计算公式、三角函数求值，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
17．已知函数$f（n）=\left\{\begin{array}{l}{n^2}（当n为奇数时）\\-{n^2}（当n为偶数时）\end{array}\right.$且an=f（n）+f（n+1），则a1+a2+…+a99等于（ ）
| A． | 0 | B． | 100 | C． | -101 | D． | -99 |
15．已知集合A={1，3，5}，B={1，m}，A∩B={1，m}，则m等于（ ）
| A． | 1 或 3 | B． | 3 或 5 | C． | 1 或 5 | D． | 1 或 3 或5 |
12．在空间直角坐标系Oxyz中，z轴上的点M到点A（1，0，2）与点B（1，-3，1）的距离相等，则点M的坐标是（ ）
| A． | （0，0，-3） | B． | （0，0，3） | C． | （0，0，$\sqrt{10}$） | D． | （0，0，-$\sqrt{10}$） |
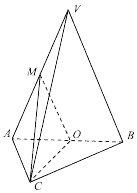如图，在三棱锥V-ABC中，平面VAB⊥平面ABC，VA=VB=4，AC=BC=2且AC⊥BC，O，M分别为AB，VA的中点．
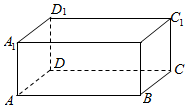如图，长方体ABCD-A1B1C1D1中，AB=12，BC=10，AA1=8，过点A1、D1的平面α与棱AB和CD分别交于点E、F，四边形A1EFD1为正方形．
17．设△ABC的内角A，B，C所对的边长分别为a，b，c，若bcosC+ccosB=2acosA，则A=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$或$\frac{2π}{3}$ |