题目内容
19.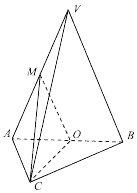 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,VA=VB=4,AC=BC=2且AC⊥BC,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,VA=VB=4,AC=BC=2且AC⊥BC,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB;
(3)求三棱锥V-ABC的体积.
分析 (1)推导出OM∥VB,由此能证明VB∥平面MOC.
(2)推导出CO⊥AB,从而CO⊥平面VAB,由此能证明平面MOC⊥平面VAB.
(3)三棱锥V-ABC的体积VV-ABC=VC-VAB,由此能求出结果.
解答 (本小题满分12分)
证明:(1)∵O,M分别为AB,VA的中点,
∵OM∥VB,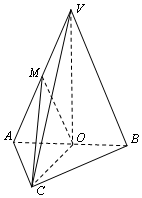
又VB?平面MOC,MO?平面MOC,
∴VB∥平面MOC. …(4分)
(2)∵AC=BC,且O是AB的中点,
∴CO⊥AB
又平面VAB⊥平面ABC,
∴CO⊥平面VAB,
又CO?平面MOC,
∴平面MOC⊥平面VAB.…(8分)
解:(3)∵AC⊥BC,且AC=BC=2,
∴$AB=\sqrt{A{C^2}+B{C^2}}=2\sqrt{2}$,
连VO,又VA=VB=4,所以$VO=\sqrt{V{A^2}-A{O^2}}=\sqrt{14}$,
由(2)知:CO⊥平面VAB,
∴三棱锥V-ABC的体积:
${V_{V-ABC}}={V_{C-VAB}}=\frac{1}{3}{S_{△VAB}}CO=\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×\sqrt{14}×\sqrt{2}=\frac{{2\sqrt{14}}}{3}$. …(12分)
点评 本题考查线面平行、线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知直线l的方程为$x-\sqrt{3}y+2=0$,则直线l的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 150° |
4.设函数$f(x)=\left\{\begin{array}{l}{2^{-x}},x≤0\\{x^{\frac{1}{2}}},x>0\end{array}\right.$,则f(-2)+f(1)=( )
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
11.已知点P(a,b)关于直线l的对称点为Q(3-b,3-a),则直线l的方程是( )
| A. | x+y-3=0 | B. | x+y+b-a=0 | C. | x+y-a-b=0 | D. | x-y+3=0 |
9.已知x≥5,则f(x)=$\frac{{x}^{2}-4x+9}{x-4}$有( )
| A. | 最大值8 | B. | 最小值10 | C. | 最大值12 | D. | 最小值14 |