求值:${log 2}^3•{log 3}^4+{({log 2}^{48}-{log 2}^3)^{\frac{1}{2}}}$．题目和参考答案——青夏教育精英家教网—

题目内容

2．求值：${log_2}^3•{log_3}^4+{（{log_2}^{48}-{log_2}^3）^{\frac{1}{2}}}$．

分析根据对数的运算法则计算即可

解答解：原式=$\frac{lg3}{lg2}•\frac{lg4}{lg3}+{（{log_2}\frac{48}{3}）^{\frac{1}{2}}}$=$\frac{2lg2}{lg2}+{4^{\frac{1}{2}}}$=2+2=4

点评本题考查了对数的运算性质，属于基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

12．设a，b是非零实数，若a＞b，则一定有（　　）

A．

$a+\frac{1}{b}＞b+\frac{1}{a}$

B．

$\frac{1}{{a{b^2}}}＞\frac{1}{{{a^2}b}}$

C．

$\frac{1}{a}＜\frac{1}{b}$

D．

ab＞b²

13．已知a=0.99³，b=log₂0.6，c=log₃π，则（　　）

10．等比数列{a_n}中，a₃+a₅=10，a₄+a₆=20
（1）求{a_n}的通项公式；
（2）设${b_n}={（-1）^n}{log_2}{a_n}$，求数列{b_n}的前29 项和S₂₉．

17．关于 x 的函数 y=a ^x，y=log_a x，其中 a＞0，a≠1，在第一象限内的图象只可能是（　　）

7．已知直线l的方程为$x-\sqrt{3}y+2=0$，则直线l的倾斜角为（　　）

14．若倾斜角为45°的直线m被平行线l₁：x+y-1=0与l₂：x+y-3=0所截得的线段为AB，则AB的长为$\sqrt{2}$．

11．已知点P（a，b）关于直线l的对称点为Q（3-b，3-a），则直线l的方程是（　　）

12．

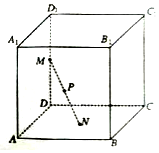如图，已知正方体ABCD-A₁B₁C₁D₁的棱长为1，长为1的线段MN的一个端点M在棱DD₁上运动，点N在正方形ABCD内运动，则MN中点P的轨迹的面积为（　　）

试题分类