题目内容
16.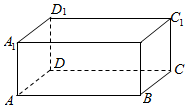 如图,长方体ABCD-A1B1C1D1中,AB=12,BC=10,AA1=8,过点A1、D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.
如图,长方体ABCD-A1B1C1D1中,AB=12,BC=10,AA1=8,过点A1、D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.(1)在图中请画出这个正方形(注意虚实线,不必写作法),并求AE的长;
(2)问平面α右侧部分是什么几何体,并求其体积.
分析 (1)利用平面与平面平行的性质,可在图中画出正方形A1EFD1,由勾股定理能求出AE的长.
(2)几何体是以A1EBB1和为底面的直四棱柱,由棱柱体积公式能求出结果.
解答 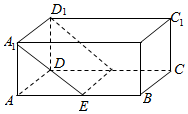 解:(1)交线围成的正方形A1EFD1如图所示(不分实虚线的酌情给分)…(3分)
解:(1)交线围成的正方形A1EFD1如图所示(不分实虚线的酌情给分)…(3分)
∵A1D1=A1E=10,A1A=8,
在Rt△A1AE中,由勾股定理知AE=6.…(6分)
(2)几何体是以A1EBB1和为底面的直四棱柱,(棱柱或四棱柱均不扣分)
由棱柱体积公式得$V=\frac{1}{2}×(6+12)×8×10=720$.…(12分)(由体积之差法也不扣分)
点评 本题考查满足条件的正方形的画法,考查棱柱的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.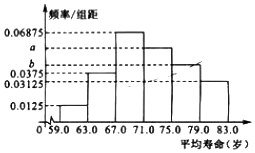 下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
(Ⅰ)请补齐频率分布表,并求出相应频率分布直方图中的a,b;
(Ⅱ)请根据统计思想,利用(Ⅰ)中的频率分布直方图估计亚洲人民的平均寿命.
 下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)| 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 |
| 阿曼 76.1 巴林 76.1 朝鲜 68.9 韩国 80.6 老挝 64.3 蒙古 67.6 缅甸 64.9 日本 82.8 | 泰国 73.7 约旦 73.4 越南 75.0 中国 74.8 伊朗 74.0 印度 66.5 文莱 77.6 也门 62.8 | 阿富汗 59.0 阿联酋 76.7 东帝汶 67.3 柬埔寨 66.4 卡塔尔 77.8 科威特 74.1 菲律宾 67.8 黎巴嫩 78.5 | 尼泊尔 68.0 土耳其 74.1 伊拉克 68.5 以色列 81.6 新加坡 81.5 叙利亚 72.3 巴基斯坦 65.2 马来西亚 74.2 | 孟加拉国 70.1 塞浦路斯 79.4 沙特阿拉伯 73.7 哈萨克斯坦68.3 印度尼西亚68.2 土库曼斯坦65.0 吉尔吉斯斯坦69.3 乌兹别克斯坦67.9 |
| 分组 | 频数 | 频率 |
| [59.0,63.0) | 2 | 0.05 |
| [63.0,67.0) | 6 | 0.15 |
| [67.0,71.0) | 11 | 0.275 |
| [71.0,75.0) | 9 | 0.225 |
| [75.0,7.0) | 7 | 0.175 |
| [79.0,83.0] | 5 | 0.125 |
| 合计 | 40 | 1.00 |
7.已知直线l的方程为$x-\sqrt{3}y+2=0$,则直线l的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 150° |
4.设函数$f(x)=\left\{\begin{array}{l}{2^{-x}},x≤0\\{x^{\frac{1}{2}}},x>0\end{array}\right.$,则f(-2)+f(1)=( )
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
11.已知点P(a,b)关于直线l的对称点为Q(3-b,3-a),则直线l的方程是( )
| A. | x+y-3=0 | B. | x+y+b-a=0 | C. | x+y-a-b=0 | D. | x-y+3=0 |
15.设F1,F2是椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}$=1(a1>b1>0)与双曲线C2:$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}$=1(a2>0,b2>0)的公共焦点,曲线C1,C2在第一象限内交于点M,∠F1MF2=90°,若椭圆C1的离心率e1∈[$\frac{{\sqrt{6}}}{3}$,1),则双曲线C2的离心率e2的范围是( )
| A. | $({1,\sqrt{3}}]$ | B. | $({1,\sqrt{2}}]$ | C. | $[{\sqrt{3},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
 如图是一个求函数值的算法流程图,若输入的x的值为5,则输出的y的值为-15.
如图是一个求函数值的算法流程图,若输入的x的值为5,则输出的y的值为-15.