��Ŀ����
��x�ᡢy��������ĵ�λ�����ֱ�Ϊ
��
������ƽ���ϵĵ�An����������
=
+
��
=2n
-
��n��N*����
��1��������{an}��ǰn���Ϊsn����sn=
•
��������{an}��ͨ�ʽ��
��2��������
�����꣬����OA1An+1��n��N*�������S��OA1An+1��������{bn}��д������{bn}��ͨ�ʽ��
��3����cn=
-2��ָ��nΪ��ֵʱ��cnȡ�����ֵ����˵�����ɣ�
| i |
| j |
| OA1 |
| i |
| j |
| AnAn+1 |
| i |
| j |
��1��������{an}��ǰn���Ϊsn����sn=
| OA1 |
| AnAn+1 |
��2��������
| OAn+1 |
��3����cn=
| bn |
| an |
���㣺ƽ������������������
ר�⣺������,�Ȳ�������ȱ�����,ƽ��������Ӧ��
��������1�������������������������ʾ�����������ֱ���������ɵ�Sn������an��Sn�Ĺ�ϵ�������������{an}��ͨ�ʽ��
��2�����������Ķ���η����Լ��ȱ����е����ʽ���õ�An+1�����꣬���������ε������ʽ���ɵõ��������Ϊ����{bn}��ͨ�ʽ��
��3���ж�����{cn}�ĵ����ԣ������������Ϊcn-cn-1�������ж����ֵ��
��2�����������Ķ���η����Լ��ȱ����е����ʽ���õ�An+1�����꣬���������ε������ʽ���ɵõ��������Ϊ����{bn}��ͨ�ʽ��
��3���ж�����{cn}�ĵ����ԣ������������Ϊcn-cn-1�������ж����ֵ��
���
�⣺��1��������sn=
•
=2n-1�٣�
��n=1ʱ��a1=s1=2 -1=1��
��n��2ʱ��sn-1=2n-1-1��
�� ��-�ڵã�an=2n-1-(2n-1-1)=2n-1��
�ֵ�n=1ʱ��a1=1�������⣬����an=2n-1��n��N*��
��2���⣺
=
+
+��+
=��1+2+22+��+2n��
+��1-1-1-��-1��
=��2n+1-1��
+��1-n��
��
���ԣ�
=(2n+1-1 �� 1-n)��
�ɵ�n��N*ʱ����OA1An+1�Ķ�������ֱ�Ϊ��
O(0��0) ��A1(1 �� 1) ��An+1(2n+1-1 �� 1-n)�ã�S��OA1An+1=
=
(2n+1+n-2)=2n+
��
��bn=2n+
��n��N*��
��3��cn=
-2=
-2=
��
��n��2ʱ��cn-cn-1=
-
=
��
��1��n��3ʱ��{cn}�ǵ������У�n��5ʱ��{cn}�ǵݼ����У�
c1��c2��c3=c4��c5��c6������cn������
�൱n=3��n=4ʱ��cnȡ�����ֵ��c3=c4=
��
| OA1 |
| AnAn+1 |
��n=1ʱ��a1=s1=2 -1=1��
��n��2ʱ��sn-1=2n-1-1��
�� ��-�ڵã�an=2n-1-(2n-1-1)=2n-1��
�ֵ�n=1ʱ��a1=1�������⣬����an=2n-1��n��N*��
��2���⣺
| OAn+1 |
| OA1 |
| A1A2 |
| AnAn+1 |
| i |
| j |
=��2n+1-1��
| i |
| j |
���ԣ�
| OAn+1 |
�ɵ�n��N*ʱ����OA1An+1�Ķ�������ֱ�Ϊ��
O(0��0) ��A1(1 �� 1) ��An+1(2n+1-1 �� 1-n)�ã�S��OA1An+1=
| 1 |
| 2 |
|
| 1 |
| 2 |
| n-2 |
| 2 |
��bn=2n+
| n-2 |
| 2 |
��3��cn=
| bn |
| an |
2n+
| ||
| 2n-1 |
| n-2 |
| 2n |
��n��2ʱ��cn-cn-1=
| n-2 |
| 2n |
| n-3 |
| 2n-1 |
| 4-n |
| 2n |
��1��n��3ʱ��{cn}�ǵ������У�n��5ʱ��{cn}�ǵݼ����У�
c1��c2��c3=c4��c5��c6������cn������
�൱n=3��n=4ʱ��cnȡ�����ֵ��c3=c4=
| 1 |
| 8 |
���������⿼��ƽ���������������������ʾ���������е�ͨ���ǰn��͵Ĺ�ϵ���������еĵ����Ե����ã��������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
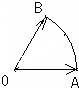 ������������Ϊ1��ƽ������
������������Ϊ1��ƽ������| OA |
| OB |
 |
| AB |
| OC |
| OA |
| OB |
| A��2 | ||||
B��
| ||||
| C��1 | ||||
D��
|
��֪����f��x���Ķ�����Ϊ��-2��2����������Ϊf�䣨x��=x2+2cosx��f��0��=0��������f��1+x��+f��x2-x����0��ʵ��x��ȡֵ��ΧΪ��������
| A����-�ޣ�+�ޣ� | ||||
| B����-1��1�� | ||||
C��(-�ޣ�1-
| ||||
D��(-1��1-
|
����A��-3��-4����B��6��3����ֱ��l��ax+y+1=0�ľ�����ȣ���ʵ��a��ֵΪ��������
A��
| ||||
B��-
| ||||
C��
| ||||
D��-
|