题目内容
把数列{n}(n∈N*),依次按第1个括号一个数,第2个括号两个数,第3个括号三个数,第4个括号四个数,第5个括号一个数,…,循环为(1),(2,3),(4,5,6),(7,8,9,10),(11),(12,13),(14,15,16),(17,18,19,20),(21),…,则第2012个括号内各数之和为 .
考点:归纳推理
专题:推理和证明
分析:括号里的数有一定规律:即每四个一组,各组里面的数都有1+2+3+4=10个数.且每四个一组的第1个括号第一个数构成一个首项为1公差为10的等差数列,设2012个括号每四个一组中第n个小组内的数,根据规律即可找出n的值.
解答:
解:括号里的数有规律:即每四个一组,里面的数都是1+2+3+4=10,
且每四个一组的第1个括号里一个数构成一个首项为1公差为10的等差数列,
故每四个一组中第n个小组内的第一个数的通项公式为:1+10(n-1)=10n-9,
设2012个括号每四个一组中第n个小组内的数,
2012÷4=503,
故第504组的第一个数为:5031,
即第2013个括号的数为:5031,
第2012个括号内的数为:(5027,5028,5029,5030),
故第2012个括号内各数之和为5027+5028+5029+5030=20114,
故答案为:20114.
且每四个一组的第1个括号里一个数构成一个首项为1公差为10的等差数列,
故每四个一组中第n个小组内的第一个数的通项公式为:1+10(n-1)=10n-9,
设2012个括号每四个一组中第n个小组内的数,
2012÷4=503,
故第504组的第一个数为:5031,
即第2013个括号的数为:5031,
第2012个括号内的数为:(5027,5028,5029,5030),
故第2012个括号内各数之和为5027+5028+5029+5030=20114,
故答案为:20114.
点评:本题是等差数列的通项公式的简单运用及等差数列的求和公式,属于基本知识的运用,试题较易.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )
一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )| A、16π | B、14π |
| C、12π | D、8π |
圆(x+2)2+(y+1)2=1关于直线y=x-1对称的圆的方程为( )
| A、x2+(y-3)2=1 |
| B、x2+(y+3)2=1 |
| C、(x-3)2+y2=1 |
| D、(x+3)2+y2=1 |
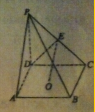
 如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.
如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.