如图.已知点P为Rt△ABC的斜边AB的延长线上一点.且PC与Rt△ABC的外接圆相切.过点C作AB的垂线.垂足为D.若PA=18.PC=6.求线段CD的长．题目和参考答案——青夏教育精英家教网—

题目内容

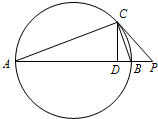如图，已知点P为Rt△ABC的斜边AB的延长线上一点，且PC与Rt△ABC的外接圆相切，过点C作AB的垂线，垂足为D，若PA=18，PC=6，求线段CD的长．

考点：与圆有关的比例线段

专题：计算题,立体几何

分析：由切割线定理解得PB=2，在Rt△POC中，由面积法得OC•PC=PO•CD，解得线段CD的长．

解答： 解：由切割线定理，得PC²=PA•PB，解得PB=2，
所以AB=16，即Rt△ABC的外接圆半径r=8，…5分
记Rt△ABC外接圆的圆心为O，连OC，则OC⊥PC，
在Rt△POC中，由面积法得OC•PC=PO•CD，解得CD=

．…10分．

点评：本题考查切割线定理，考查面积法的运用，比较基础．

练习册系列答案

新课程单元检测新疆电子音像出版社系列答案

相关题目

设函数f（x）的定义域为D，若任取x₁∈D，存在唯一的x₂∈D，满足

f(x1)+f(x2)

=C，则称C为函数y=f（x）在D上的均值，给出下列五个函数：①y=x；②y=x²；③y=4sinx；④y=lgx；⑤y=2^x．则所有满足在其定义域上的均值为2的函数的序号为

已知直线l：x+y=m和曲线C：y²=4（x+4）（-4≤x≤4）．
（1）直线l与曲线C相交于两点，求m的取值范围；
（2）设直线l与曲线C相交于A，B，求△AOB面积的最大值．

已知f（x）=x-sinx，求证：若x，θ∈（0，π），则

=1的左右焦点，A是双曲线在第一象限内的点，若|AF₂|=4且∠F₁AF₂=60°，延长AF₂交双曲线右支于点B，则△F₁AB的面积等于

．

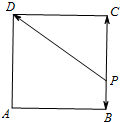如图，正方形ABCD的边长为2，点P是线段BC上的动点，则（

）•

的最小值为

．

已知函数f（x）=ax+lnx（a∈R）
（Ⅰ）求函数f（x）的单调递增区间
（Ⅱ）已知g（x）=4^x-3•2^x+1，若对任意的m∈（0，+∞），存在n∈[0，1]，使得f（m）＜g（n），求实数a的取值范围．

试题分类