题目内容
tan(α-β)=
,tanβ=-
,则sin2α= .
| 1 |
| 2 |
| 1 |
| 7 |
考点:二倍角的正弦,两角和与差的正切函数
专题:计算题,三角函数的求值
分析:由两角和与差的正切函数公式化简已知可得tanα的值,从而由万能公式化简所求后代入即可求值.
解答:
解:∵tan(α-β)=
=
=
,
∴可解得:tanα=
,
∴sin2α=
=
=
.
故答案为:
.
| tanα-tanβ |
| 1+tanαtanβ |
tanα+
| ||
1-
|
| 1 |
| 2 |
∴可解得:tanα=
| 1 |
| 3 |
∴sin2α=
| 2tanα |
| 1-tan2α |
2×
| ||
1-
|
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考察了两角和与差的正切函数公式,万能公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
tan(-570°)+sin240°=( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知全集U=R,集合A={x|1≤x≤3},B={x|x>2},则A∩∁UB等于( )
| A、{x|1<x≤2} |
| B、{x|1≤x<2} |
| C、{x|1≤x≤2} |
| D、{x|1≤x≤3} |
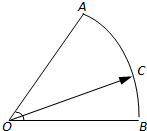 如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若
如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若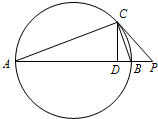 如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.
如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.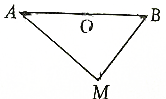 如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明
如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明