题目内容
已知函数f(x)=ax+lnx(a∈R)
(Ⅰ)求函数f(x)的单调递增区间
(Ⅱ)已知g(x)=4x-3•2x+1,若对任意的m∈(0,+∞),存在n∈[0,1],使得f(m)<g(n),求实数a的取值范围.
(Ⅰ)求函数f(x)的单调递增区间
(Ⅱ)已知g(x)=4x-3•2x+1,若对任意的m∈(0,+∞),存在n∈[0,1],使得f(m)<g(n),求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(Ⅰ)先求出函数导数,通过讨论①当a≥0时,②当a<0时的情况,从而求出函数的单调区间;
(Ⅱ)分别求出f(x),g(x)的最大值,问题转化为f(x)max<g(x)max,即-1+ln(-
)<-1,从而求出a的范围.
(Ⅱ)分别求出f(x),g(x)的最大值,问题转化为f(x)max<g(x)max,即-1+ln(-
| 1 |
| a |
解答:
解(Ⅰ)∵f(x)=ax+lnx,x∈(0,+∞),∴f′(x)=a+
,
①当a≥0时,f′(x)=a+
>0∴f(x)在(0,+∞)上单调递增,
②当a<0时,f′(x)=a+
>0⇒
>-a⇒x<-
,
∴f(x)在(0,-
)上单调递增,
综上:当a≥0时,f(x)的增区间是(0,+∞),当a<0时,f(x)的增区间是(0,-
);
(Ⅱ)g(x)=4x-3•2x+1,x∈[0,1],令2x=t∈[1,2],
y=t2-3t+1,t∈[1,2],当t=1或2时,ymax=-1,
由(Ⅰ)知,当a≥0时,f(x)在(0,+∞)上单调递增,无最值,不可能满足f(m)<g(n),
当a<0时,在(0,-
)上递增,在(-
,+∞)上递减;
∴f(x)max=f(-
)=-1+ln(-
),
∵对任意的m∈(0,+∞),存在n∈[0,1],使得f(m)<g(n),
∴f(x)max<g(x)max,∴-1+ln(-
)<-1,
∴ln(-
)<0,
∴-
<1,∴a<-1.
| 1 |
| x |
①当a≥0时,f′(x)=a+
| 1 |
| x |
②当a<0时,f′(x)=a+
| 1 |
| x |
| 1 |
| x |
| 1 |
| a |
∴f(x)在(0,-
| 1 |
| a |
综上:当a≥0时,f(x)的增区间是(0,+∞),当a<0时,f(x)的增区间是(0,-
| 1 |
| a |
(Ⅱ)g(x)=4x-3•2x+1,x∈[0,1],令2x=t∈[1,2],
y=t2-3t+1,t∈[1,2],当t=1或2时,ymax=-1,
由(Ⅰ)知,当a≥0时,f(x)在(0,+∞)上单调递增,无最值,不可能满足f(m)<g(n),
当a<0时,在(0,-
| 1 |
| a |
| 1 |
| a |
∴f(x)max=f(-
| 1 |
| a |
| 1 |
| a |
∵对任意的m∈(0,+∞),存在n∈[0,1],使得f(m)<g(n),
∴f(x)max<g(x)max,∴-1+ln(-
| 1 |
| a |
∴ln(-
| 1 |
| a |
∴-
| 1 |
| a |
点评:本题考查了函数的单调性,函数的最值问题,考查了导数的应用,考查了转化思想,是一道中档题.

练习册系列答案
相关题目
tan(-570°)+sin240°=( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
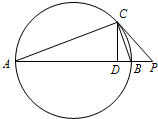 如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.
如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.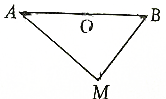 如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明
如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明