题目内容
已知直线l:x+y=m和曲线C:y2=4(x+4)(-4≤x≤4).
(1)直线l与曲线C相交于两点,求m的取值范围;
(2)设直线l与曲线C相交于A,B,求△AOB面积的最大值.
(1)直线l与曲线C相交于两点,求m的取值范围;
(2)设直线l与曲线C相交于A,B,求△AOB面积的最大值.
考点:抛物线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)联立
,化为x2-(4+2m)x+m2-16=0,令△=0,解得m=-5.把x=4代入抛物线方程可得y2=4×8,取y=-4
.把(4,-4
)代入直线x+y=m,可得m=4-4
.即可得出m的取值范围.
(2)设A(x1,y1),B(x2,y2).由(1)可得x1+x2=4+2m,x1x2=m2-16.利用弦长公式可得|AB|=
=4
.利用点到直线的距离公式可得原点O到直线l的距离d=
.利用S△OAB=
d•|AB|=2
.令f(m)=m3+5m2,m∈(-5,4-4
].利用导数研究其单调性极值与最值即可得出.
|
| 2 |
| 2 |
| 2 |
(2)设A(x1,y1),B(x2,y2).由(1)可得x1+x2=4+2m,x1x2=m2-16.利用弦长公式可得|AB|=
| (1+1)[(x1+x2)2-4x1x2] |
| 2m+10 |
| |m| | ||
|
| 1 |
| 2 |
| m2(m+5) |
| 2 |
解答:
解:(1)联立
,化为x2-(4+2m)x+m2-16=0,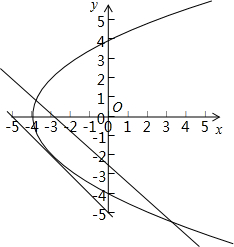
令△=(4+2m)2-4(m2-16)=0,解得m=-5.
把x=4代入抛物线方程可得y2=4×8,取y=-4
.
把(4,-4
)代入直线x+y=m,可得m=4-4
.
∴-5<m≤4-4
.
∴m的取值范围是(-5,4-4
];
(2)设A(x1,y1),B(x2,y2).
由(1)可得x1+x2=4+2m,x1x2=m2-16.
∴|AB|=
=
=4
.
原点O到直线l的距离d=
.
∴S△OAB=
d•|AB|
=
×
×4
=2
.
令f(m)=m3+5m2,m∈(-5,4-4
].
f′(m)=3m2+10m=3m(m+
).
令f′(m)>0,解得-5<m<-
,此时函数f(m)单调递增;令f′(m)<0,解得-
<m≤4-4
,此时函数f(m)单调递减.
∴当m=-
时,函数f(m)取得极大值即最大值
.
∴△AOB面积取得最大值2
=
.
|
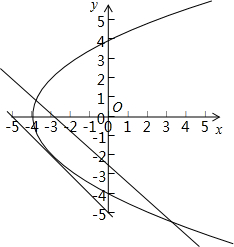
令△=(4+2m)2-4(m2-16)=0,解得m=-5.
把x=4代入抛物线方程可得y2=4×8,取y=-4
| 2 |
把(4,-4
| 2 |
| 2 |
∴-5<m≤4-4
| 2 |
∴m的取值范围是(-5,4-4
| 2 |
(2)设A(x1,y1),B(x2,y2).
由(1)可得x1+x2=4+2m,x1x2=m2-16.
∴|AB|=
| (1+1)[(x1+x2)2-4x1x2] |
| 2[(4+2m)2-4(m2-16)] |
| 2m+10 |
原点O到直线l的距离d=
| |m| | ||
|
∴S△OAB=
| 1 |
| 2 |
=
| 1 |
| 2 |
| -m | ||
|
| 2m+10 |
=2
| m2(m+5) |
令f(m)=m3+5m2,m∈(-5,4-4
| 2 |
f′(m)=3m2+10m=3m(m+
| 10 |
| 3 |
令f′(m)>0,解得-5<m<-
| 10 |
| 3 |
| 10 |
| 3 |
| 2 |
∴当m=-
| 10 |
| 3 |
| 500 |
| 27 |
∴△AOB面积取得最大值2
|
20
| ||
| 9 |
点评:本题考查了抛物线的标准方程及其性质、直线与抛物线相交转化为方程联立可得△≥0及其根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知直线a,平面α,β,且a?α,则“a⊥β”是“α⊥β”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
tan(-570°)+sin240°=( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
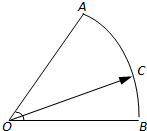 如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若
如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若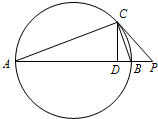 如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.
如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.