题目内容
已知F1,F2分别是双曲线x2-
=1的左右焦点,A是双曲线在第一象限内的点,若|AF2|=4且∠F1AF2=60°,延长AF2交双曲线右支于点B,则△F1AB的面积等于 .
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:根据双曲线的定义,得|AF1|-|AF2|=2a=2,△AF1F2中根据余弦定理算出|F1F2|2,从而得到c2=7.设A(x1,y1),B(x2,y2).由直线AB方程与双曲线方程联解,可得B的坐标,由△F1AB的面积S=
×2c×|y1-y2|,计算即可得到.
| 1 |
| 2 |
解答:
解:如图所示,由双曲线的方程可知:a=1.
∴|AF1|-|AF2|=2,
∵|AF2|=4,∴|AF1|=6.
∴|F1F2|2=(2c)2=62+42-2×6×4×cos60°,
即有c2=7,
∴b2=c2-1=6,
设A(x1,y1),B(x2,y2).
则
,化为7x12-2
x1-15=0,
解得x1=
,或x1=-
(舍去).
由此解出A的坐标为(
,
),
直线AB的斜率为k=
=-3
.
设直线AB方程为y=-3
(x-
),与双曲线6x2-y2=6联解,
得到B(
,-
),
∴△ABF1的面积S=
×2
×|y1-y2|=
×|
+
|=24
.
故答案为:24
.

∴|AF1|-|AF2|=2,
∵|AF2|=4,∴|AF1|=6.
∴|F1F2|2=(2c)2=62+42-2×6×4×cos60°,
即有c2=7,
∴b2=c2-1=6,
设A(x1,y1),B(x2,y2).
则
|
| 7 |
解得x1=
5
| ||
| 7 |
3
| ||
| 7 |
由此解出A的坐标为(
5
| ||
| 7 |
6
| ||
| 7 |
直线AB的斜率为k=
| ||||||
|
| 3 |
设直线AB方程为y=-3
| 3 |
| 7 |
得到B(
13
| ||
| 7 |
18
| ||
| 7 |
∴△ABF1的面积S=
| 1 |
| 2 |
| 7 |
| 7 |
6
| ||
| 7 |
18
| ||
| 7 |
| 3 |
故答案为:24
| 3 |
点评:本题给出双曲线的焦点三角形△AF1F2的两边之长和夹角,求△F1AB的面积.着重考查了双曲线的定义与标准方程、直线与圆锥曲线位置关系和三角形的面积公式等知识点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,若在双曲线的右支上存在点P,满足|PF2|=|F1F2|,且原点O到直线PF1的距离等于双曲线的实半轴长,则该双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、4x±3y=0 |
| B、3x±5y=0 |
| C、3x±4y=0 |
| D、5x±3y=0 |
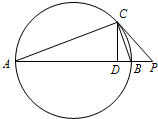 如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.
如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.