题目内容
已知向量
=（-1，2，4），
=（x，-1，-2），并且
⊥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
考点：向量的数量积判断向量的共线与垂直
专题：空间向量及应用
分析：由于
⊥
，可得
•
=0，解出即可．
| a |
| b |
| a |
| b |
解答：
解：∵
⊥
，
∴
•
=-x-2-8=0，
解得x=-10．
故选：B．
| a |
| b |
∴
| a |
| b |
解得x=-10．
故选：B．
点评：本题考查了向量垂直与数量积的关系，属于基础题．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
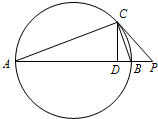如图，已知点P为Rt△ABC的斜边AB的延长线上一点，且PC与Rt△ABC的外接圆相切，过点C作AB的垂线，垂足为D，若PA=18，PC=6，求线段CD的长．
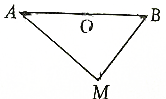如图所示，已知O是线段AB的中点，M是平面上任意一点，试证明已知函数f（x）是奇函数，且f（x）=
，当2≤x＜3时，f（x）=（
）x，则f（2014）=（ ）
| 1 |
| f(x+3) |
| 1 |
| 2 |
| A、2 | ||
| B、4 | ||
| C、-4 | ||
D、-
|