题目内容
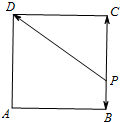如图，正方形ABCD的边长为2，点P是线段BC上的动点，则（| PB |
| PD |
| PC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：建立平面直角坐标系A-xy，设P（2，x），则
=（0，-x），x∈[0，2]，
=（-2，2-x），
=（0，2-x），利用x 表示（
+
）•
的函数求最值．
| PB |
| PD |
| PC |
| PB |
| PD |
| PC |
解答：
解：建立平面直角坐标系A-xy，设P（2，x），
则
=（0，-x），x∈[0，2]，
=（-2，2-x），
=（0，2-x），
所以（
+
）•
=2x2-6x+4=2（x-1.5）2+4-4.5，
因为x∈[0，2]，
所以x=1.5时，（
+
）•
的最小值为-0.5即-
；
故答案为：-
．
则
| PB |
| PD |
| PC |
所以（
| PB |
| PD |
| PC |
因为x∈[0，2]，
所以x=1.5时，（
| PB |
| PD |
| PC |
| 1 |
| 2 |
故答案为：-
| 1 |
| 2 |
点评：本题考查了向量的数量积以及二次函数闭区间的最值，关键是建立坐标系，将问题转化为二次函数的最值求法．
练习册系列答案
全优点练单元计划系列答案
相关题目
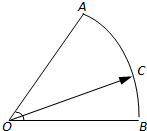如图，在扇形OAB中，∠AOB=60°，C为弧AB上的一个动点．若
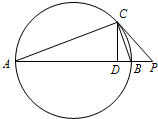如图，已知点P为Rt△ABC的斜边AB的延长线上一点，且PC与Rt△ABC的外接圆相切，过点C作AB的垂线，垂足为D，若PA=18，PC=6，求线段CD的长．
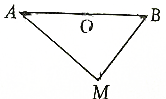如图所示，已知O是线段AB的中点，M是平面上任意一点，试证明