题目内容
已知f(x)=x-sinx,求证:若x,θ∈(0,π),则
≥f(
).
| 2f(θ)+f(x) |
| 3 |
| 2θ+x |
| 3 |
考点:利用导数求闭区间上函数的最值
专题:证明题,导数的综合应用
分析:构造函数g(x)=
-f(
),求导g′(x)=
(1-cosx)-
(1-cos
)=
(cos
-cosx),从而可得gmin(x)=g(θ)=0;从而证明.
| 2f(θ)+f(x) |
| 3 |
| 2θ+x |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2θ+x |
| 3 |
| 1 |
| 3 |
| 2θ+x |
| 3 |
解答:
证明:构造函数g(x)=
-f(
),
则g′(x)=
(1-cosx)-
(1-cos
)
=
(cos
-cosx)
又∵y=cosx在(0,π)上单调,
故
=x;故x=θ;
∴x∈(0,θ),g′(x)<0,x∈(θ,π),g′(x)>0;
故g(x)在(0,θ)上单调递减,在(θ,π)上单调递增;
∴gmin(x)=g(θ)=0;
∴x∈[0,π]时,g(x)≥g(θ)=0;
故若x,θ∈(0,π),则
≥f(
).
| 2f(θ)+f(x) |
| 3 |
| 2θ+x |
| 3 |
则g′(x)=
| 1 |
| 3 |
| 1 |
| 3 |
| 2θ+x |
| 3 |
=
| 1 |
| 3 |
| 2θ+x |
| 3 |
又∵y=cosx在(0,π)上单调,
故
| 2θ+x |
| 3 |
∴x∈(0,θ),g′(x)<0,x∈(θ,π),g′(x)>0;
故g(x)在(0,θ)上单调递减,在(θ,π)上单调递增;
∴gmin(x)=g(θ)=0;
∴x∈[0,π]时,g(x)≥g(θ)=0;
故若x,θ∈(0,π),则
| 2f(θ)+f(x) |
| 3 |
| 2θ+x |
| 3 |
点评:本题考查了导数的综合应用,属于基础题.

练习册系列答案
相关题目
已知全集U=R,集合A={x|1≤x≤3},B={x|x>2},则A∩∁UB等于( )
| A、{x|1<x≤2} |
| B、{x|1≤x<2} |
| C、{x|1≤x≤2} |
| D、{x|1≤x≤3} |
若M为△ABC的重心,点D,E,F分别为三边BC,AB,AC的中点,则
+
+
等于( )
| MA |
| MB |
| MC |
A、6
| ||
B、-6
| ||
C、
| ||
D、6
|
已知函数f(x)是奇函数,且f(x)=
,当2≤x<3时,f(x)=(
)x,则f(2014)=( )
| 1 |
| f(x+3) |
| 1 |
| 2 |
| A、2 | ||
| B、4 | ||
| C、-4 | ||
D、-
|
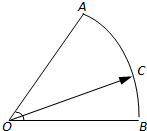 如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若
如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若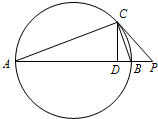 如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.
如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,过点C作AB的垂线,垂足为D,若PA=18,PC=6,求线段CD的长.