题目内容
7.某年级星期一至星期五每天下午排3节课,每天下午随机选择1节作为综合实践课(上午不排该课程),张老师与王老师分别任教甲、乙两个班的综合实践课程.(1)求这两个班“在星期一不同时上综合实践课”的概率;
(2)设这两个班“在一周中同时上综合实践课的节数”为X,求X的概率分布表与数学期望E(X).
分析 (1)利用对立事件的概率关系求解;
(2)两个班“在一星期的任一天同时上综合实践课”的概率为$\frac{1}{3}$,一周中5天是5次独立重复试验,服从二项分布.
解答 解:(1)这两个班“在星期一不同时上综合实践课”的概率为$P=1-\frac{3}{3×3}=\frac{2}{3}$.…(4分)
(2)由题意得$X\~B(5,\frac{1}{3})$,$P(X=k)=C_5^k{({\frac{1}{3}})^k}{({\frac{2}{3}})^{5-k}},k=0,1,2,3,4,5$.…(6分)
所以X的概率分布表为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{32}{243}$ | $\frac{80}{243}$ | $\frac{80}{243}$ | $\frac{40}{243}$ | $\frac{10}{243}$ | $\frac{1}{243}$ |
所以,X的数学期望为$E(X)=5×\frac{1}{3}=\frac{5}{3}$.…(10分)
点评 本题考查了古典概型的概率,独立重复试验的分布列、期望,属于中档题.

练习册系列答案
相关题目
12.已知函数$f(x)=3cos(ωx+\frac{π}{3})(ω>0)$和g(x)=2sin(2x+φ)+1的图象的对称轴完全相同,若$x∈[0,\frac{π}{3}]$,则f(x)的取值范围是( )
| A. | [-3,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-3,\frac{{3\sqrt{3}}}{2}]$ | D. | $[-3,\frac{3}{2}]$ |
19.随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到A类工人生产能力的茎叶图(图1),B类工人生产能力的频率分布直方图(图2).
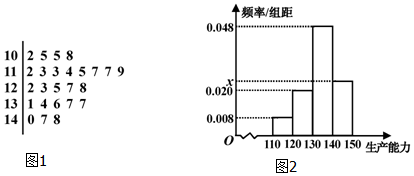
(Ⅰ)问A类、B类工人各抽查了多少工人,并求出直方图中的x;
(Ⅱ)求A类工人生产能力的中位数,并估计B类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ) 若规定生产能力在[130,150]内为能力优秀,由以上统计数据在答题卡上完成下面的2×2列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.
能力与培训时间列联表
参考数据:
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.

(Ⅰ)问A类、B类工人各抽查了多少工人,并求出直方图中的x;
(Ⅱ)求A类工人生产能力的中位数,并估计B类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ) 若规定生产能力在[130,150]内为能力优秀,由以上统计数据在答题卡上完成下面的2×2列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.
能力与培训时间列联表
| 短期培训 | 长期培训 | 合计 | |
| 能力优秀 | 8 | 54 | 62 |
| 能力不优秀 | 17 | 21 | 38 |
| 合计 | 25 | 75 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如表:
(1)请将表中数据补充完整,并直接写出函数f(x)的解析式;
(2)若将函数f(x)的图象上所有点的横坐标变为原来的2倍,纵坐标不变,得到函数g(x)的图象,求当x∈[-$\frac{π}{3}$,$\frac{π}{3}$]时,函数g(x)的值域;
(3)若将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=h(x)的图象,若=h(x)图象的一个对称中心为($\frac{π}{12},0$),求θ的最小值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 3 | 0 | -3 | 0 |
(2)若将函数f(x)的图象上所有点的横坐标变为原来的2倍,纵坐标不变,得到函数g(x)的图象,求当x∈[-$\frac{π}{3}$,$\frac{π}{3}$]时,函数g(x)的值域;
(3)若将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=h(x)的图象,若=h(x)图象的一个对称中心为($\frac{π}{12},0$),求θ的最小值.

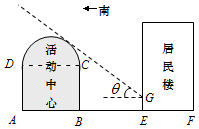 如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足$tanθ=\frac{3}{4}$.
如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足$tanθ=\frac{3}{4}$.