题目内容
17.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如表:| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 3 | 0 | -3 | 0 |
(2)若将函数f(x)的图象上所有点的横坐标变为原来的2倍,纵坐标不变,得到函数g(x)的图象,求当x∈[-$\frac{π}{3}$,$\frac{π}{3}$]时,函数g(x)的值域;
(3)若将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=h(x)的图象,若=h(x)图象的一个对称中心为($\frac{π}{12},0$),求θ的最小值.
分析 (1)由表中数据列关于ω、φ的二元一次方程组,求得A、ω、φ的值,得到函数解析式,进一步完成数据补充.
(2)根据函数y=Asin(ωx+φ)的图象变换规律可求g(x),利用正弦函数的性质可求其值域.
(3)由(1)及函数y=Asin(ωx+φ)的图象变换规律得g(x),令2x+2θ+$\frac{π}{6}$=kπ,解得x=$\frac{kπ}{2}-\frac{π}{12}$-θ,k∈Z.令:$\frac{kπ}{2}-\frac{π}{12}$-θ=$\frac{π}{12}$,结合θ>0即可解得θ的最小值.
解答 解:(1)根据表中已知数据,解得A=3,ω=2,φ=$\frac{π}{6}$,
数据补全如下表:
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 3 | 0 | -3 | 0 |
(2)将函数f(x)的图象上所有点的横坐标变为原来的2倍,纵坐标不变,
得到图象对于的函数解析式为:g(x)=3sin(x+$\frac{π}{6}$).
由x∈[-$\frac{π}{3}$,$\frac{π}{3}$],可得:x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{π}{2}$],可得:sin(x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
可得:函数g(x)=3sin(x+$\frac{π}{6}$)∈[-$\frac{3}{2}$,3].
(3)若将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=h(x)的图象,若h(x)图象的一个对称中心为($\frac{π}{12},0$),
由(Ⅰ)知f(x)=3sin(2x+$\frac{π}{6}$),得g(x)=3sin(2x+2θ+$\frac{π}{6}$).
因为y=sinx的对称中心为(kπ,0),k∈Z.
令2x+2θ+$\frac{π}{6}$=kπ,解得x=$\frac{kπ}{2}-\frac{π}{12}$-θ,k∈Z.
由于函数y=g(x)的图象关于点($\frac{π}{12}$,0)成中心对称,令:$\frac{kπ}{2}-\frac{π}{12}$-θ=$\frac{π}{12}$,
解得θ=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z.由θ>0可知,当k=1时,θ取得最小值$\frac{π}{3}$.
点评 本题考查了由y=Asin(ωx+φ)的部分图象求解函数解析式,函数y=Asin(ωx+φ)的图象变换规律的应用,考查了正弦函数的图象和性质的应用,其中关键是要根据图象分析出函数的最值,周期等,进而求出A,ω和φ值,属于中档题.

练习册系列答案
相关题目
8.一个几何体的三视图如图所示,那么该几何体是( )


| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 四棱柱 |
9.2016年下半年,锦阳市教体局举行了市教育系统直属单位职工篮球比赛,以增强直属单位间的交流与合作,组织方统计了来自A1,A2,A3,A4,A5等5个直属单位的男子篮球队的平均身高与本次比赛的平均得分,如表所示:
(1)根据表中数据,求y关于x的线性回归方程;(系数精确到0.01)
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
| 单位 | A1 | A2 | A3 | A4 | A5 |
| 平均身高x(单位:cm) | 170 | 174 | 176 | 181 | 179 |
| 平均得分y | 62 | 64 | 66 | 70 | 68 |
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
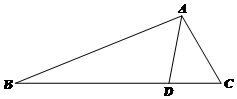 如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.
如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.