题目内容
12.已知函数$f(x)=3cos(ωx+\frac{π}{3})(ω>0)$和g(x)=2sin(2x+φ)+1的图象的对称轴完全相同,若$x∈[0,\frac{π}{3}]$,则f(x)的取值范围是( )| A. | [-3,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-3,\frac{{3\sqrt{3}}}{2}]$ | D. | $[-3,\frac{3}{2}]$ |
分析 先求出f(x)的解析式,再结合余弦函数的单调性,即可求出f(x)的取值范围.
解答 解:因为函数f(x)和g(x)的图象的对称轴完全相同,故f(x)和g(x)的周期相同,所以ω=2,
所以$f(x)=3cos(2x+\frac{π}{3})$,
由$x∈[0,\frac{π}{3}]$,得$2x+\frac{π}{3}∈[\frac{π}{3},π]$,根据余弦函数的单调性,当$2x+\frac{π}{3}=π$,
即$x=\frac{π}{3}$时,f (x)min=-3,
当$2x+\frac{π}{3}=\frac{π}{3}$,即x=0时,f (x)max=$\frac{3}{2}$,
所以f (x)的取值范围是$[-3,\frac{3}{2}]$,
故选D.
点评 本题考查三角函数的图象与性质,考查学生的计算能力,确定函数的解析式是关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.已知直线l:y=x-1,双曲线c1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,抛物线c2:y2=2x,直线l与c1相交于A,B两点,与c2交于C,D两点,若线段AB与CD的中点相同,则双曲线c1的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\sqrt{3}$ |
1.在“二十四节气入选非遗”宣传活动中,从甲、乙、丙三位同学中任选两人介绍一年中时令、气候、物候等方面的变化规律,那么甲同学被选中的概率为( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
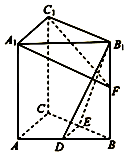 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.