题目内容
15．设{an}是等差数列，若a4+a5+a6=21，则S9=63．分析 由等差数列的通项公式求出a5=7，再由等差数列的前n项和公式得${S}_{9}=\frac{9}{2}（{a}_{1}+{a}_{9}）=9{a}_{5}$，由此能求出结果．
解答 解：∵{an}是等差数列，a4+a5+a6=21，
∴a4+a5+a6=3a5=21，解得a5=7，
∴${S}_{9}=\frac{9}{2}（{a}_{1}+{a}_{9}）=9{a}_{5}$=63．
故答案为：63．
点评 本题考查等差数列的前9项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
6．复数z满足z（2+i）=3-i，则复数z在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．已知直线l：y=x-1，双曲线c1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，抛物线c2：y2=2x，直线l与c1相交于A，B两点，与c2交于C，D两点，若线段AB与CD的中点相同，则双曲线c1的离心率为（ ）
| A． | $\frac{\sqrt{6}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{15}}{3}$ | D． | $\sqrt{3}$ |
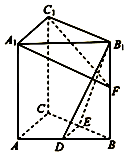如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱BB1上，且B1D⊥A1F，A1C1⊥A1B1．