题目内容
18．若等比数列{an}满足a2a4=a5，a4=8，则公比q=2，前n项和Sn=2n-1．分析 利用等比数列通项公式列出方程组，求出首项和公比，由此能求出首项和前n项和．
解答 解：∵等比数列{an}满足a2a4=a5，a4=8，
∴$\left\{\begin{array}{l}{{a}_{1}q•{a}_{1}{q}^{3}={a}_{1}{q}^{4}}\\{{a}_{1}{q}^{3}=8}\end{array}\right.$，
解得a1=1，q=2，
∴前n项和Sn=$\frac{1×（1-{2}^{n}）}{1-2}$=2n-1．
故答案为：2，2n-1．
点评 本题考查等比数列的首项和前n项和的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
应用题作业本系列答案
相关题目
8．某同学的父亲决定今年夏天卖西瓜赚钱，根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如表：
（1）求这五天内所卖西瓜个数的平均值和方差；
（2）求变量x．y之间的线性回归方程，并预测当温度为30℃时所卖西瓜的个数．
附：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$（精确到0.1）
| 温度x（℃） | 32 | 33 | 35 | 37 | 38 |
| 西瓜个数y | 20 | 22 | 24 | 30 | 34 |
（2）求变量x．y之间的线性回归方程，并预测当温度为30℃时所卖西瓜的个数．
附：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$（精确到0.1）
9．复数z=（a+i）（-3+ai）（a∈R），若z＜0，则a的值是（ ）
| A． | a=$\sqrt{3}$ | B． | a=-$\sqrt{3}$ | C． | a=-1 | D． | a=1 |
6．
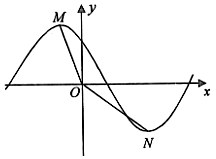将函数y=$\sqrt{3}$sin（$\frac{π}{4}$x）的图象向左平移3个单位，得函数y=$\sqrt{3}$sin（$\frac{π}{4}$x+φ）（|φ|＜π）的图象（如图），点M，N分别是函数f（x）图象上y轴两侧相邻的最高点和最低点，设∠MON=θ，则tan（φ-θ）的值为（ ）
将函数y=$\sqrt{3}$sin（$\frac{π}{4}$x）的图象向左平移3个单位，得函数y=$\sqrt{3}$sin（$\frac{π}{4}$x+φ）（|φ|＜π）的图象（如图），点M，N分别是函数f（x）图象上y轴两侧相邻的最高点和最低点，设∠MON=θ，则tan（φ-θ）的值为（ ）| A． | 1-$\sqrt{3}$ | B． | 2-$\sqrt{3}$ | C． | 1+$\sqrt{3}$ | D． | -2+$\sqrt{3}$ |
13．已知集合A={x|x（x+1）≤0}，集合B={x|x＞0}，则A∪B=（ ）
| A． | {x|x≥-1} | B． | {x|x＞-1} | C． | {x|x≥0} | D． | {x|x＞0} |