题目内容
3.已知实数u,v,x,y满足u2+v2=1,$\left\{\begin{array}{l}x+y-1≥0\\ x-2y+2≥0\\ x≤2\end{array}\right.$,则z=ux+vy的最大值是2$\sqrt{2}$.分析 画出约束条件的可行域,求出角点坐标,利用三角代换求解目标函数的最大值即可.
解答  解:约束条件的$\left\{\begin{array}{l}x+y-1≥0\\ x-2y+2≥0\\ x≤2\end{array}\right.$可行域如图三角形区域:A(2,1),B(2,-1),C(0,1),u2+v2=1
解:约束条件的$\left\{\begin{array}{l}x+y-1≥0\\ x-2y+2≥0\\ x≤2\end{array}\right.$可行域如图三角形区域:A(2,1),B(2,-1),C(0,1),u2+v2=1
设u=sinθ,v=cosθ,
目标函数经过A时,z=2sinθ+2cosθ=2$\sqrt{2}$sin($θ+\frac{π}{4}$)$≤2\sqrt{2}$.
目标函数经过B时,z=2sinθ-cosθ=$\sqrt{5}$sin(θ+β)$≤\sqrt{5}$.(其中tanβ=$\frac{\sqrt{5}}{5}$).
目标函数经过C时,z=sinθ≤1.
所以目标函数的最大值为:2$\sqrt{2}$.
故答案为:$2\sqrt{2}$.
点评 本题考查线性规划的简单应用,“角点法”以及三角函数的化简求解最值是解题的关键,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.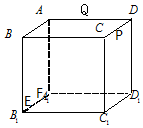 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )| A. | 与x,y,z都有关 | B. | 与x有关,与y,z无关 | ||
| C. | 与y有关,与x,z无关 | D. | 与z有关,与x,y无关 |
12.方程x-log${\;}_{\frac{1}{2}}$x=3和x-log${\;}_{\frac{1}{3}}$x=3的根分别为α,β,则有( )
| A. | α<β | B. | α>β | ||
| C. | α=β | D. | 无法确定α与β大小 |
13.已知等差数列{an}满足a1+a2+a3+…+a101=0,则有( )
| A. | a51=51 | B. | a2+a100<0 | C. | a1+a101>0 | D. | a3+a99=0 |
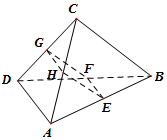 (理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC
(理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC