题目内容
8.某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如表:| 温度x(℃) | 32 | 33 | 35 | 37 | 38 |
| 西瓜个数y | 20 | 22 | 24 | 30 | 34 |
(2)求变量x.y之间的线性回归方程,并预测当温度为30℃时所卖西瓜的个数.
附:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$(精确到0.1)
分析 (1)由总数除以天数得平均数,根据方差公式,代入可得方差;
(2)根据公式求回归系数,可得回归方程;x=30,代入计算,可预测当温度为30℃时所卖西瓜的个数.
解答 解:(1)$\overline{y}$=$\frac{20+22+24+30+34}{5}$=26,
方差为s2=$\frac{1}{5}×$[(20-26)2+(22-26)2+(24-26)2+(30-26)2+(34-26)2]=27.2.
(2)$\overline{x}$=35,$\sum_{i=1}^{5}{{x}_{i}}^{2}$=6151,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=4608,
所以$\stackrel{∧}{b}$=$\frac{4608-5×35×26}{6151-5×3{5}^{2}}$≈2.2,$\stackrel{∧}{a}$=25-2.2×35=-51,
所以回归直线方程为$\stackrel{∧}{y}$=2.2x-51,
当x=30时,$\stackrel{∧}{y}$=15,所以预测当温度为30℃时所卖西瓜的个数为15.
点评 本题考查平均值和方差,考查线性回归方程,正确计算是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.高三年级有8个班级,分派4位数学老师任教,每个教师教两个班,则不同的分派方法有( )
| A. | ${P}_{8}^{2}$${P}_{6}^{2}$${P}_{4}^{2}$${P}_{2}^{2}$ | B. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$ | ||
| C. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$${P}_{4}^{4}$ | D. | $\frac{C_8^2C_6^2C_4^2C_2^2}{4!}$ |
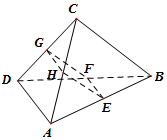 (理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC
(理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC