题目内容
10.在数列{an}中,a1=1,若${a_{n+1}}=2{a_n}+2(n∈{N^*})$,则an=3•2n-1-2.分析 两边同加1,可得an+1+2=2(an+2),从而{an+2}是以a1+2=3为首项,q=2为公比的等比数列,故可求an.
解答 解:由题意an+1=2an+2,可得an+1+2=2(an+2),
∴{an+2}是以a1+2=3为首项,q=2为公比的等比数列
∴an+2=3•2n-1,故an=3•2n-1-2,
故答案为3•2n-1-2.
点评 本题以数列递推式为载体,考查等比数列,关键是运用整体思想,把{an+2}看成数列的通项,进行求解,也可以看成是等价转化成等比数列的一种解题方法.

练习册系列答案
相关题目
20.高三年级有8个班级,分派4位数学老师任教,每个教师教两个班,则不同的分派方法有( )
| A. | ${P}_{8}^{2}$${P}_{6}^{2}$${P}_{4}^{2}$${P}_{2}^{2}$ | B. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$ | ||
| C. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$${P}_{4}^{4}$ | D. | $\frac{C_8^2C_6^2C_4^2C_2^2}{4!}$ |
1.已知集合A={-2,-1,0,1,2},∁RB={x|(x-1)(x+2)≥0},则A∩B=( )
| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0} | D. | {-2,1,2} |
5.据报道,巴基斯坦由中方投资运营的瓜达尔港目前已通航.这是一个可以停靠8~10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.有消息称,瓜达尔港的月货物吞吐量将是目前天津、上海两港口月货物吞吐量之和.表格记录了2015年天津、上海两港口的月吞吐量(单位:百万吨):

(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;
(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;
(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设X为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出X的数学期望(不需要计算过程).
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
| 天津 | 24 | 22 | 26 | 23 | 24 | 26 | 27 | 25 | 28 | 24 | 25 | 26 |
| 上海 | 32 | 27 | 33 | 31 | 30 | 31 | 32 | 33 | 30 | 32 | 30 | 30 |

(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;
(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;
(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设X为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出X的数学期望(不需要计算过程).
15.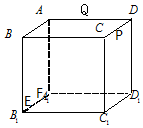 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )| A. | 与x,y,z都有关 | B. | 与x有关,与y,z无关 | ||
| C. | 与y有关,与x,z无关 | D. | 与z有关,与x,y无关 |
20.在空间中,下列命题正确的是( )
| A. | 若平面α内有无数条直线与直线l平行,则l∥α | |
| B. | 若平面α内有无数条直线与平面β平行,则α∥β | |
| C. | 若平面α内有无数条直线与直线l垂直,则l⊥α | |
| D. | 若平面α内有无数条直线与平面β垂直,则α⊥β |