题目内容
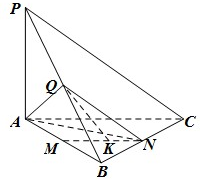 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.(1)证明:直线QK∥平面PAC;
(2)若PA=AB=BC,求二面角Q-AN-M的平面角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(1)连结QM,由已知条件推导出平面QMN∥平面PAC,由此能证明QK∥平面PAC.
(2)过M作MH⊥AN于H,连QH,则∠QHM即为二面角Q-AN-M的平面角,由此能求出二面角Q-AN-M的平面角的余弦值.
(2)过M作MH⊥AN于H,连QH,则∠QHM即为二面角Q-AN-M的平面角,由此能求出二面角Q-AN-M的平面角的余弦值.
解答:
(1)证明:连结QM,∵点Q,M,N分别是线段PB,AB,BC的中点,
∴QM∥PA,MN∥AC,QM∥平面PAC,MN∥平面PAC,
∵MN∩QM=M,∴平面QMN∥平面PAC,QK?平面QMN,
∴QK∥平面PAC.
(2)解:过M作MH⊥AN于H,连QH,
则∠QHM即为二面角Q-AN-M的平面角,
令PA=AB=BC=2,则QM=AM=1,
∴此时sin∠MAH=sin∠BAN=
,MH=
,
记二面角Q-AN-M的平面角为θ,
则tanθ=
=
,∴cosθ=
,
∴二面角Q-AN-M的平面角的余弦值为
.
∴QM∥PA,MN∥AC,QM∥平面PAC,MN∥平面PAC,
∵MN∩QM=M,∴平面QMN∥平面PAC,QK?平面QMN,
∴QK∥平面PAC.
(2)解:过M作MH⊥AN于H,连QH,
则∠QHM即为二面角Q-AN-M的平面角,
令PA=AB=BC=2,则QM=AM=1,
∴此时sin∠MAH=sin∠BAN=
| 1 | ||
|
| 1 | ||
|
记二面角Q-AN-M的平面角为θ,
则tanθ=
| QM |
| MH |
| 5 |
| ||
| 6 |
∴二面角Q-AN-M的平面角的余弦值为
| ||
| 6 |
点评:本题考查直线与平面平行的证明,考查二面角的平面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
若α是第三象限的角,则
是( )
| α |
| 3 |
| A、第一、二、三象限角 |
| B、第一、二、四象限角 |
| C、第一、三、四象限角 |
| D、第二、三、四象限角 |
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其众数为a,中位数为b,平均数为c,则有( )
| A、c>a>b |
| B、a>b>c |
| C、b>c>a |
| D、c>b>a |
从只有3张中奖的10张彩票中不放回随机逐张抽取,设X表示直至抽到中奖彩票时的次数,则P(X=3)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
将下列各式按大小顺序排列,其中正确的是( )
A、cos0<cos
| ||
B、cos0<cos
| ||
C、cos0>cos
| ||
D、cos0>cos
|
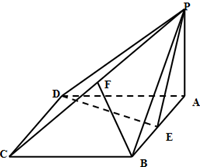 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.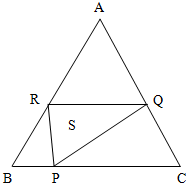 如图,在正△ABC的边BC、CA、AB上分别取点P、Q、R,使CQ=2BP,AR=3BP.已知正三角形的边长是11cm,BP=xcm,△PQR的面积为S
如图,在正△ABC的边BC、CA、AB上分别取点P、Q、R,使CQ=2BP,AR=3BP.已知正三角形的边长是11cm,BP=xcm,△PQR的面积为S