题目内容
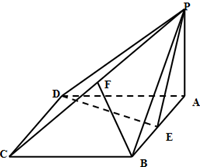 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.(Ⅰ)求证:面PDE⊥面PAB;
(Ⅱ)求证:BF∥面PDE.
(Ⅲ)当PA=AB时,
①求直线PC与平面ABCD所成角的大小.
②求二面角P-DE-A所成角的正弦值的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定,平面与平面垂直的判定
专题:空间角
分析:(I)证明DE⊥AB,PA⊥DE,利用线面垂直的判定定理,可得DE⊥面PAB,从而可证面PDE⊥面PAB.
(Ⅱ)证明FG与BE平行且相等,可得BF∥GE,利用线面平行的判定可得BF∥面PDE.
(Ⅲ)①设AB=2,由已知条件推导出∠ACP是直线PC与平面ABCD所成的角,分别求出AC和AP,利用正切函数能求出直线PC与平面ABCD所成角的大小.
②以A为原点,AD为x轴,平面ABCD内过A垂直AD的直线为y轴,AO为z轴,建立空间直线坐标系,利用向量法能求出二面角P-DE-A所成的角的正弦值.
(Ⅱ)证明FG与BE平行且相等,可得BF∥GE,利用线面平行的判定可得BF∥面PDE.
(Ⅲ)①设AB=2,由已知条件推导出∠ACP是直线PC与平面ABCD所成的角,分别求出AC和AP,利用正切函数能求出直线PC与平面ABCD所成角的大小.
②以A为原点,AD为x轴,平面ABCD内过A垂直AD的直线为y轴,AO为z轴,建立空间直线坐标系,利用向量法能求出二面角P-DE-A所成的角的正弦值.
解答:
(Ⅰ)证明:∵四棱锥P-ABCD的底面ABCD是菱形,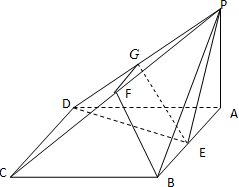
∠BCD=60°,PA⊥面ABCD,E是AB的中点,
∴DE⊥AB,PA⊥DE,
∵AB∩PA=A,∴DE⊥平面PAB,
∵DE?平面PDE,∴面PDE⊥面PAB.
(Ⅱ)证明:取PD的中点G,连结FG,GE,
∵F,G是中点,∴FG∥CD,且FG=
CD,
∴FG与BE平行且相等,∴BF∥GE,
∵GE?面PDE,BF不包含于平面PDE,
∴BF∥面PDE.
(Ⅲ)① 设AB=2,
设AB=2,
∵四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,
PA⊥面ABCD,E是AB的中点,F是PC的中点,PA=AB,
∴∠ACP是直线PC与平面ABCD所成的角,
∴AC=
=2
,AP=2,
∴tan∠ACP=
=
,∴∠ACP=30°,
∴直线PC与平面ABCD所成角为30°.
②以A为原点,AD为x轴,平面ABCD内过A垂直AD的直线为y轴,
AO为z轴,建立空间直线坐标系,设AB=2,
由题意知P(0,0,2),D(2,0,0),E(
,
,0),
A(0,0,0),∴
=(2,0,-2),
=(
,
,-2),
=(0,0,2),
设平面PDE的法向量
=(x,y,z),
则
,
取x=1,得
=(1,
,1),
∵AP⊥平面ABCD,∴
=(0,0,2)是平面ADE的一个法向量,
设二面角P-DE-A所成角的平面角为θ,
则cosθ=|cos<
,
>|=|
|=
,
∴sinθ=
=
.
∴二面角P-DE-A所成的角的正弦值为
.

∠BCD=60°,PA⊥面ABCD,E是AB的中点,
∴DE⊥AB,PA⊥DE,
∵AB∩PA=A,∴DE⊥平面PAB,
∵DE?平面PDE,∴面PDE⊥面PAB.
(Ⅱ)证明:取PD的中点G,连结FG,GE,
∵F,G是中点,∴FG∥CD,且FG=
| 1 |
| 2 |
∴FG与BE平行且相等,∴BF∥GE,
∵GE?面PDE,BF不包含于平面PDE,
∴BF∥面PDE.
(Ⅲ)①
 设AB=2,
设AB=2,∵四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,
PA⊥面ABCD,E是AB的中点,F是PC的中点,PA=AB,
∴∠ACP是直线PC与平面ABCD所成的角,
∴AC=
| 4+4-2×2×2×cos120° |
| 3 |
∴tan∠ACP=
| 2 | ||
2
|
| ||
| 3 |
∴直线PC与平面ABCD所成角为30°.
②以A为原点,AD为x轴,平面ABCD内过A垂直AD的直线为y轴,
AO为z轴,建立空间直线坐标系,设AB=2,
由题意知P(0,0,2),D(2,0,0),E(
| 1 |
| 2 |
| ||
| 2 |
A(0,0,0),∴
| PD |
| PE |
| 1 |
| 2 |
| ||
| 2 |
| AP |
设平面PDE的法向量
| n |
则
|
取x=1,得
| n |
| 3 |
∵AP⊥平面ABCD,∴
| AP |
设二面角P-DE-A所成角的平面角为θ,
则cosθ=|cos<
| n |
| AP |
| 2 | ||
2×
|
| 1 | ||
|
∴sinθ=
1-(
|
2
| ||
| 5 |
∴二面角P-DE-A所成的角的正弦值为
2
| ||
| 5 |
点评:本题考查平面与平面垂直的证明,考查直线与平面平行的证明,考查直线与平面所成的角的求法,考查二面角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
某市的纬度是北纬21°34′,小王想在某住宅小区买房,该小区的楼高7层,每层3m,楼与楼间相距15m,要使所买楼房在一年四季正午的太阳不被前面的楼房遮挡,应该选购该楼的最低层数是( )
| A、1 | B、2 | C、3 | D、4 |
已知角α的终边经过点(3a,-4a)(a<0),则sinα+cosα等于( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
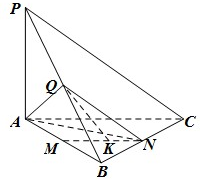 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.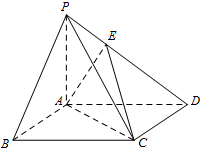 如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA=AB=2,PB=PD=2
如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA=AB=2,PB=PD=2