题目内容
10名工人某天生产同一零件，生产的件数是15，17，14，10，15，17，17，16，14，12，设其众数为a，中位数为b，平均数为c，则有（ ）
| A、c＞a＞b |
| B、a＞b＞c |
| C、b＞c＞a |
| D、c＞b＞a |
考点：众数、中位数、平均数
专题：概率与统计
分析：根据众数，中位数和平均数的定义和公式分别进行计算，即可得到结论．
解答：
解；将数据从小到大重新排好为，10，12，14，14，15，15，16，17，17，17．
则众数a=17，中位数b=15，
平均数c=15+
（-5-3-1-1+0+0+2+2+2）=15-0.4=14.6，
∴a＞b＞c，
故选：B．
则众数a=17，中位数b=15，
平均数c=15+
| 1 |
| 10 |
∴a＞b＞c，
故选：B．
点评：本题主要考查众数，中位数和平均数的计算和比较大小，根据定义分别求出即可，将数据从小到大重新排列是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
设△ABC的内角A，B，C所对的边分别为a，b，c，且C=
，a+b=λ，若△ABC面积的最大值为9
，则λ的值为（ ）
| π |
| 3 |
| 3 |
| A、8 | B、12 | C、16 | D、21 |
某市的纬度是北纬21°34′，小王想在某住宅小区买房，该小区的楼高7层，每层3m，楼与楼间相距15m，要使所买楼房在一年四季正午的太阳不被前面的楼房遮挡，应该选购该楼的最低层数是（ ）
| A、1 | B、2 | C、3 | D、4 |
计算
dx的结果是（ ）
| ∫ | e 1 |
| 1 |
| x |
| A、e |
| B、1-e-2 |
| C、1 |
| D、e-1 |
下列命题中，真命题是（ ）
A、a+b=0的充要条件是
| ||
| B、?x0∈R，x02≤0 | ||
| C、?x∈R，2x＞1 | ||
| D、ab＞0是a＞0，b＞0的充分条件 |
某产品的广告费用x与销售额y的统计数据如下表：
根据上表可得回归方程
=
x+
中的
为9.4，据此模型预报广告费用为6万元时销售额为（ ）
| 广告费用x（万元） | 3.5 | 3.8 | 4 | 4.7 |
| 销售费用x（万元） | 27 | 37 | 47 | 49 |
 |
| y |
|
| b |
|
| a |
|
| b |
| A、63.6万元 |
| B、58.8万元 |
| C、67.7万元 |
| D、72.0万元 |
已知角α的终边经过点（3a，-4a）（a＜0），则sinα+cosα等于（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
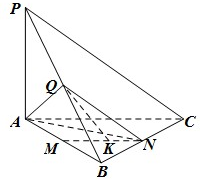如图，在三棱锥P-ABC中，直线PA⊥平面ABC，且∠ABC=90°，又点Q，M，N分别是线段PB，AB，BC的中点，且点K是线段MN上的动点．