题目内容
已知圆C的方程为x2+y2=4,过点M(2,4)作圆C的两条切线,切点分别为A,B,直线AB恰好经过椭圆T:
+
=1(a>b>0)的右顶点和上顶点.
(1)求椭圆T的方程;
(2)已知直线l:y=kx+
(k>0)与椭圆相交于P,Q两点,O为坐标原点,求△OPQ面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆T的方程;
(2)已知直线l:y=kx+
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)利用点到直线的距离公式,求得另一条切线方程,与圆方程联立,从而可得直线AB的方程,由此可求椭圆T的方程;
(2)直线方程与椭圆方程联立,利用韦达定理求出|PQ|,求出原点到直线l的距离,表示出三角形的面积,进而利用基本不等式,即可求得△OPQ面积的最大值.
(2)直线方程与椭圆方程联立,利用韦达定理求出|PQ|,求出原点到直线l的距离,表示出三角形的面积,进而利用基本不等式,即可求得△OPQ面积的最大值.
解答:
解:(1)由题意:一条切线方程为:x=2,设另一条切线方程为:y-4=k(x-2).(2分)
则:
=2,解得k=
,此时切线方程为:y=
x+
,
切线方程与圆方程联立,可得x2+(
x+
)2=4,
从而可得x=-
,y=
,
则直线AB的方程为x+2y=2….(4分)
令x=0,解得y=1,∴b=1;令y=0,得x=2,∴a=2
故所求椭圆方程为
+y2=1.….(6分)
(2)联立
,整理得(1+4k2)x2+8
kx+8=0,
令P(x1,y1),Q(x2,y2),则x1+x2=-
,x1x2=
,
△=(8
k)2-32(1+4k2)>0,即:2k2-1>0…..(8分)
又原点到直线l的距离为d=
,|PQ|=
|x1-x2|,….(10分)
∴S△OPQ=
|PQ|d=
|x2-x1|
=
=2
•
=2
•
=2
•
≤1,
当且仅当k=
时取等号,∴△OPQ面积的最大值为1.….(12分)
则:
| |4-2k| | ||
|
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
切线方程与圆方程联立,可得x2+(
| 3 |
| 4 |
| 5 |
| 2 |
从而可得x=-
| 6 |
| 5 |
| 8 |
| 5 |
则直线AB的方程为x+2y=2….(4分)
令x=0,解得y=1,∴b=1;令y=0,得x=2,∴a=2
故所求椭圆方程为
| x2 |
| 4 |
(2)联立
|
| 3 |
令P(x1,y1),Q(x2,y2),则x1+x2=-
8
| ||
| 1+4k2 |
| 8 |
| 1+4k2 |
△=(8
| 3 |
又原点到直线l的距离为d=
|
| ||
|
| 1+k2 |
∴S△OPQ=
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
(-
|
=2
| 6 |
|
=2
| 6 |
|
=2
| 6 |
|
当且仅当k=
| ||
| 2 |
点评:本题考查椭圆的标准方程,考查直线与圆相切,考查三角形面积的计算,考查基本不等式的运用,正确表示三角形的面积是关键.

练习册系列答案
相关题目
矩形ABCD中AB与BC长度之比为2:3,在矩形ABCD内任取一点P,则使∠APB<90°的概率为( )
A、
| ||
B、
| ||
C、1-
| ||
D、1-
|
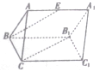 三棱柱ABC-A1B1C1的各棱相等,AA1⊥底面ABC,E是AA1的中点.
三棱柱ABC-A1B1C1的各棱相等,AA1⊥底面ABC,E是AA1的中点.