题目内容
已知点M(0,1),C(2,3),动点P满足|
|=1,过点M且斜率为k的直线l与动点P的轨迹相交于A、B两点.
(1)求动点P的轨迹方程;
(2)求实数k的取值范围;
(3)求证:
•
为定值;
(4)若O为坐标原点,且
•
=12,求直线l的方程.
| PC |
(1)求动点P的轨迹方程;
(2)求实数k的取值范围;
(3)求证:
| MA |
| MB |
(4)若O为坐标原点,且
| OA |
| OB |
考点:直线与圆锥曲线的综合问题,平面向量数量积的运算
专题:圆锥曲线中的最值与范围问题
分析:(1)设P(x,y),由已知得
=1,由此能求出动点P的轨迹方程.
(2)设直线l的方程为y=kx+1,代入动点P的轨迹方程得:(1+k2)x2-4(1+k)x+7=0,由此利用根的判别式能求出实数k的取值范围.
(3)设过M点的圆切线为MT,T为切点,由MT2=MA×MB,能证明
•
为定值.
(4)设A(x1,y1),B(x2,y2),由韦达定理得
•
=x1x2+y1y2=
+8=12,由此能求出直线l的方程.
| (x-2)2+(y-3)2 |
(2)设直线l的方程为y=kx+1,代入动点P的轨迹方程得:(1+k2)x2-4(1+k)x+7=0,由此利用根的判别式能求出实数k的取值范围.
(3)设过M点的圆切线为MT,T为切点,由MT2=MA×MB,能证明
| MA |
| MB |
(4)设A(x1,y1),B(x2,y2),由韦达定理得
| OA |
| OB |
| 4k(k+1) |
| 1+k2 |
解答:
(1)解:设P(x,y),
∵点M(0,1),C(2,3),动点P满足|
|=1,
∴
=1,
整理,得动点P的轨迹方程为:(x-2)2+(x-3)2=1.…(2分)
(2)解:直线l过点M(0,1),且斜率为k,
则直线l的方程为y=kx+1,…(3分)
将其代入动点P的轨迹方程得:(1+k2)x2-4(1+k)x+7=0,
由题意:△=[-4(1+k)]2-28(1+k2)>0,
解得
<k<
.…(6分)
(3)证明:设过M点的圆切线为MT,T为切点,
则MT2=MA×MB,
而MT2=(0-2)2+(1-3)2=7,…(8分)
∴
•
=|
|•|
|cos0°=7为定值.…(10分)
(4)解:设A(x1,y1),B(x2,y2),
由(1)知
,…(10分)
•
=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1
=
+8=12,…(12分)
解得k=1,当k=1时.△=82-4×2×7=8,…(13分)
故k=1,直线l的方程为y=x+1.…(14分)
∵点M(0,1),C(2,3),动点P满足|
| PC |
∴
| (x-2)2+(y-3)2 |
整理,得动点P的轨迹方程为:(x-2)2+(x-3)2=1.…(2分)
(2)解:直线l过点M(0,1),且斜率为k,
则直线l的方程为y=kx+1,…(3分)
将其代入动点P的轨迹方程得:(1+k2)x2-4(1+k)x+7=0,
由题意:△=[-4(1+k)]2-28(1+k2)>0,
解得
4-
| ||
| 3 |
4+
| ||
| 3 |
(3)证明:设过M点的圆切线为MT,T为切点,
则MT2=MA×MB,
而MT2=(0-2)2+(1-3)2=7,…(8分)
∴
| MA |
| MB |
| MA |
| MB |
(4)解:设A(x1,y1),B(x2,y2),
由(1)知
|
| OA |
| OB |
=
| 4k(k+1) |
| 1+k2 |
解得k=1,当k=1时.△=82-4×2×7=8,…(13分)
故k=1,直线l的方程为y=x+1.…(14分)
点评:本题考查动点的轨迹方程的求法,考查直线斜率的取值范围的求法,考查
•
为定值的证明,考查直线方程的求法,解题时要注意根的判断式、韦达定理的合理运用.
| MA |
| MB |

练习册系列答案
相关题目
已知直线l⊥平面α,P∈α,那么过点P且垂直于l的直线( )
| A、只有一条,在平面α内 |
| B、只有一条,且不在平面α内 |
| C、有无数条,且都在平面α内 |
| D、有无数条,不一定都在平面α内 |
设平面向量
=(4,-3),
=(2,1)若
+t
与
的夹角是
,求实数t的值( )
| a |
| b |
| a |
| b |
| b |
| π |
| 4 |
| A、-3 | B、1 |
| C、-3或1 | D、以上都不对 |
函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2+1,则f(-1)等于( )
| A、1 | B、-1 | C、2 | D、-2 |
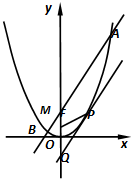 如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.
如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.