题目内容
已知椭圆Г的方程为
+
=1(a>b>0)点A,B分别为Г上的两个动点,O为坐标原点,且OA⊥OB;其中OA,OB称为椭圆的一条半径.
(1)求证:
+
=
+
;|OA|2+|OB|2的最小值为
;
(2)过点O作OH⊥AB于H,求证:|OH|=
;S△OAB的最小值是
;
(3)将(1)(2)的结论推广至双曲线,结论是否依然成立,若成立,证明你的结论;若不成立,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求证:
| 1 |
| |OA|2 |
| 1 |
| |OB|2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 4a2b2 |
| a2+b2 |
(2)过点O作OH⊥AB于H,求证:|OH|=
| ab | ||
|
| a2b2 |
| a2+b2 |
(3)将(1)(2)的结论推广至双曲线,结论是否依然成立,若成立,证明你的结论;若不成立,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:计算题,不等式的解法及应用,圆锥曲线的定义、性质与方程
分析:(1)以O为极点,x轴的正半轴为极轴建立极坐标系,求出椭圆的极坐标方程为ρ2(b2cos2θ+a2sin2θ)=a2b2,设A(ρ1,θ),B(ρ2,θ+
),运用三角函数的平方关系和诱导公式,以及基本不等式,即可得到;
(2)运用直角三角形的面积公式,结合勾股定理和(1)的结论,即可得证;
(3)求出双曲线的极坐标方程,运用(1)(2)的方法,即可得到类似的结论.
| π |
| 2 |
(2)运用直角三角形的面积公式,结合勾股定理和(1)的结论,即可得证;
(3)求出双曲线的极坐标方程,运用(1)(2)的方法,即可得到类似的结论.
解答:
(1)证明:以O为极点,x轴的正半轴为极轴建立极坐标系,
则椭圆的极坐标方程为ρ2(b2cos2θ+a2sin2θ)=a2b2,
设A(ρ1,θ),B(ρ2,θ+
),
则
+
=
+
=
+
=
=
=
+
;
|OA|2+|OB|2=
+
=
[(b2cos2θ+a2sin2θ)+(b2sin2θ+a2cos2θ)](
+
)
=
(2+
+
)≥
,
即有|OA|2+|OB|2的最小值为
.
(2)证明:由三角形的面积公式,可得:|OH|=
=
=
=
=
,
S△OAB=
|OH|•|AB|=
•
≥
•
=
,
即有S△OAB的最小值是
;
(3)解:类似椭圆的做法,得到结论:已知双曲线的方程为
-
=1(b>a>0),
点A,B分别为双曲线上的两个动点,O为坐标原点,且OA⊥OB,
则有①
+
=
-
,|OA|2+|OB|2的最小值为
,
②过点O作OH⊥AB于H,则|OH|=
;S△OAB的最小值是
.
则将(1)(2)的结论推广至双曲线,结论不依然成立,
理由是双曲线的极坐标方程为ρ2(b2cos2θ-a2sin2θ)=a2b2,且b>a,
运用(1)、(2)的方法,即可得到上面的两个结论.
则椭圆的极坐标方程为ρ2(b2cos2θ+a2sin2θ)=a2b2,
设A(ρ1,θ),B(ρ2,θ+
| π |
| 2 |
则
| 1 |
| |OA|2 |
| 1 |
| |OB|2 |
| 1 |
| ρ12 |
| 1 |
| ρ22 |
| b2cos2θ+a2sin2θ |
| a2b2 |
b2cos2(θ+
| ||||
| a2+b2 |
=
| a2(sin2θ+cos2θ)+b2(cos2θ+sin2θ) |
| a2b2 |
| a2+b2 |
| a2b2 |
| 1 |
| a2 |
| 1 |
| b2 |
|OA|2+|OB|2=
| a2b2 |
| b2cos2θ+a2sin2θ |
| a2b2 |
| b2sin2θ+a2cos2θ |
=
| 1 |
| a2+b2 |
| a2b2 |
| b2cos2θ+a2sin2θ |
| a2b2 |
| b2sin2θ+a2cos2θ |
=
| a2b2 |
| a2+b2 |
| b2cos2θ+a2sin2θ |
| b2sin2θ+a2cos2θ |
| b2sin2θ+a2cos2θ |
| b2cos2θ+a2sin2θ |
| 4a2b2 |
| a2+b2 |
即有|OA|2+|OB|2的最小值为
| 4a2b2 |
| a2+b2 |
(2)证明:由三角形的面积公式,可得:|OH|=
| |OA|•|OB| |
| |AB| |
| |OA|•|OB| | ||
|
=
|
|
| ab | ||
|
S△OAB=
| 1 |
| 2 |
| ab | ||
2
|
| |OA|2+|OB|2 |
| ab | ||
2
|
| 2ab | ||
|
| a2b2 |
| a2+b2 |
即有S△OAB的最小值是
| a2b2 |
| a2+b2 |
(3)解:类似椭圆的做法,得到结论:已知双曲线的方程为
| x2 |
| a2 |
| y2 |
| b2 |
点A,B分别为双曲线上的两个动点,O为坐标原点,且OA⊥OB,
则有①
| 1 |
| |OA|2 |
| 1 |
| |OB|2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 4a2b2 |
| b2-a2 |
②过点O作OH⊥AB于H,则|OH|=
| ab | ||
|
| a2b2 | ||
|
则将(1)(2)的结论推广至双曲线,结论不依然成立,
理由是双曲线的极坐标方程为ρ2(b2cos2θ-a2sin2θ)=a2b2,且b>a,
运用(1)、(2)的方法,即可得到上面的两个结论.
点评:本题考查椭圆的方程的运用,考查椭圆的极坐标方程的应用,考查三角函数的化简及求值,考查基本不等式的运用,考查化简运算能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
三条直线x=2,x-y-1=0,x+ky=0相交于一点,则实数k=( )
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
设数列{an}是等比数列,函数y=x2-x-2的两个零点是a2,a3,则a1a4=( )
| A、2 | B、1 | C、-1 | D、-2 |
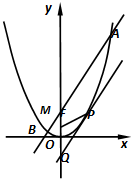 如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.
如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.