题目内容
设a为g(x)=
x3+2x2-3x-1的极值点,且函数f(x)=
,则f(
)+f(log2
)的值等于 .
| 4 |
| 3 |
|
| 1 |
| 4 |
| 1 |
| 6 |
考点:利用导数研究函数的极值
专题:计算题,函数的性质及应用
分析:令g′(x)=0,可得极值点,由题意可求a值,从而可得函数f(x)解析式,利用对数运算性质可求答案.
解答:
解:g′(x)=4x2+4x-3=(2x-1)(2x+3),
令g′(x)=0,得x=
或x=-
,
由题意可知a=
,
∴f(x)=
,
∴f(
)+f(log2
)=log
+(
)log2
=2+2log26=2+6=8,
故答案为:8.
令g′(x)=0,得x=
| 1 |
| 2 |
| 3 |
| 2 |
由题意可知a=
| 1 |
| 2 |
∴f(x)=
|
∴f(
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 6 |
故答案为:8.
点评:该题考查利用导数研究函数的极值、分段函数求值,考查对数的运算性质,属基础题.

练习册系列答案
相关题目
椭圆的长轴长为10,一个焦点坐标为(4,0),则它的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=x3+ax2+x在(0,+∞)有两个极值点,则实数a的取值范围是( )
A、(-∞,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-∞,-
|
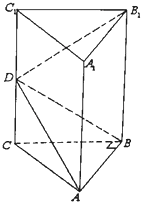 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点