题目内容

3．某几何体的三视图如图所示，则该几何体的外接球的体积为（　　）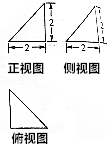
A．12πB．4$\sqrt{3}$πC．48πD．32$\sqrt{3}π$

分析 由已知的三视图可得：该几何体是一个以俯视图为底面的三棱锥，其外接球相当于一个棱长为2的正方体的外接球，计算出球的半径，代入球的体积公式，可得答案．

解答 解：由已知的三视图可得：该几何体是一个以俯视图为底面的三棱锥，
其外接球为棱长为2的正方体的外接球，
故外接球的半径R=$\sqrt{3}$，
故球的体积V=$\frac{4}{3}π（\sqrt{3}）^{3}$=$4\sqrt{3}π$；
故选B．

点评 本题考查的知识点是由三视图求体积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
13．下面几种推理过程是演绎推理的是（　　）
A．由平面三角形的性质推测空间三棱锥的性质
B．所有的金属都能够导电，铀是金属，所以铀能够导电
C．高一参加军训有12个班，1班51人，2班53人，三班52人，由此推测各班都超过50人
D．在数列{an}中，a1=2，an=2an-1+1（n≥2），由此归纳出{an}的通项公式
14．某学院的A，B，C三个专业共有1500名学生，为了调查这些学生勤工俭学的情况，拟采用分层抽样的方法抽取一个容量为150的样本．已知该学院的A专业有420名学生，B专业有580名学生，则在该学院的C专业应抽取50名学生．
11．已知一组数据按从小到大的顺序排列为：14，19，x，23，27，其中中位数是22，则x的值为（　　）
A．24B．23C．22D．21
18．已知平面内A，B，C，D这4个点中任何3个点都不在一条直线上，写出由其中每3点为顶点的所有三角形．
8．函数f（x）=3sin（2x-$\frac{π}{3}$）（x∈R）的图象为C，如下结论中正确的是①②③④⑤（写出所在正确结论的编号）．
①图象C关于直线x=$\frac{11}{12}$π对称；
②图象C关于点（$\frac{2π}{3}$，0）对称；
③函数f（x）在区间（-$\frac{π}{12}$，$\frac{5π}{12}$）内是增函数；
④由f（x1）=f（x2）=0可得x1-x2必是$\frac{π}{4}$的整数倍；
⑤函数y=f（x）的表达式可以改写为f（x）=3cos（2x+$\frac{7π}{6}$）；
⑥将图象C向左平移$\frac{π}{3}$个单位长度后得到的函数为奇函数．
15．把一枚硬币连续抛掷3次，恰好有两次反面向上的概率为$\frac{3}{8}$．
12．已知函数y=f（x）在x=x0处可导，则$\underset{lim}{h→∞}\frac{f（{x}_{0}+h）-f（{x}_{0}-h）}{h}$等于（　　）
A．f′（x0）B．2f′（x0）C．-2f′（x0）D．0
4．△ABC中，内角A、B、C所对的边分别为a、b、c，且acosB-bcosA=$\frac{1}{2}$c，则$\frac{tanA}{tanB}$=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网