��Ŀ����
8������f��x��=3sin��2x-$\frac{��}{3}$����x��R����ͼ��ΪC�����½�������ȷ���Ǣ٢ڢۢܢݣ�д��������ȷ���۵ı�ţ�����ͼ��C����ֱ��x=$\frac{11}{12}$�жԳƣ�
��ͼ��C���ڵ㣨$\frac{2��}{3}$��0���Գƣ�
�ۺ���f��x�������䣨-$\frac{��}{12}$��$\frac{5��}{12}$��������������
����f��x1��=f��x2��=0�ɵ�x1-x2����$\frac{��}{4}$����������
�ݺ���y=f��x���ı���ʽ���Ը�дΪf��x��=3cos��2x+$\frac{7��}{6}$����
��ͼ��C����ƽ��$\frac{��}{3}$����λ���Ⱥ�õ��ĺ���Ϊ�溯����
���� �Ƚ����Ǻ������л���Ȼ��ֱ��������Ǻ�����ͼ�κ�����ȥ�жϣ��ٽ�$x=\frac{11��}{12}$���룬�Ƚ��Dz�����ֵ���ڽ���$��\frac{2��}{3}��0��$���뺯�������㼴Ϊ�Գ����ģ������ú����ĵ�����ȥ�ж����䣮��������������ڽ����жϣ��ݸ������Ǻ������յ���ʽ����ת���жϣ���ͨ��ƽ�ƽ�����Ǻ�������ż�Խ����жϣ�
��� �⣺�ٵ�x=$\frac{11}{12}$��ʱ��f��$\frac{11}{12}$�У�=3sin��2��$\frac{11}{12}$��-$\frac{��}{3}$��=3sin$\frac{3��}{2}$=-3Ϊ��Сֵ������$x=\frac{11��}{12}$�Ǻ�����һ���Գ��ᣬ���Ԣ���ȷ��
�ڵ�$x=\frac{2��}{3}$ʱ��f��$\frac{2��}{3}$��=3sin��2��$\frac{2��}{3}$-$\frac{��}{3}$��=3sin��=0������ͼ��C���ڵ�$��\frac{2��}{3}��0��$�Գƣ����Ԣ���ȷ��
�۵�$-\frac{��}{12}��x��\frac{5��}{12}$ʱ��$-\frac{��}{6}��2x��\frac{5��}{6}��-\frac{��}{2}��2x-\frac{��}{3}��\frac{��}{2}$����ʱ�����������������Ԣ���ȷ��
�ܺ���������T=$\frac{2��}{2}=��$������f��x1��=f��x2��=0�ɵ�x1-x2=k$•\frac{T}{2}$=$\frac{k��}{2}$����x1-x2����$\frac{��}{2}$�����������ʢ���ȷ��
��f��x��=3sin��2x-$\frac{��}{3}$��=3cos[$\frac{��}{2}$-��2x-$\frac{��}{3}$��]=3cos��$\frac{5}{6}$��-2x��=3cos��2x-$\frac{5}{6}$�У�=3cos��2x+2��-$\frac{5}{6}$�У�=3cos��2x+$\frac{7��}{6}$�����ʢ���ȷ��
����y=3sin2x��ͼ������ƽ��$\frac{��}{3}$����λ���ȣ��õ�y=3sin[2��x+$\frac{��}{3}$��-$\frac{��}{3}$]=3sin��2x+$\frac{��}{3}$������ʱ����Ϊ�����ż�������ʢ���
������ȷ���Ǣ٢ڢۢܢ�
�ʴ�Ϊ���٢ڢۢܢݣ�
���� ���⿼�����Ǻ�����ͼ������ʣ������ø����ǹ�ʽ�����Ǻ������л���Ȼ�����о���Ӧ�����ʣ��ۺϿ������Ǻ��������ʣ�


| A�� | $\frac{28}{3}$�� | B�� | $\frac{20}{3}$�� | C�� | 4�� | D�� | $\frac{8}{3}$�� |
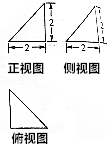
| A�� | 12�� | B�� | 4$\sqrt{3}$�� | C�� | 48�� | D�� | 32$\sqrt{3}��$ |
| A�� | $\frac{n-2}{2n��n+1��}$ | B�� | $\frac{2{n}^{2}+1}{4n+1}$ | ||
| C�� | ��$\sqrt{n+1}$-$\sqrt{n}$��$\sqrt{n}$ | D�� | $\frac{1+4+7+��+��3n-2��}{2{n}^{2}}$ |
| A�� | -$\frac{4}{3}$ | B�� | -$\frac{3}{4}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{4}{3}$ |