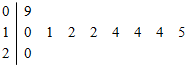题目内容

18．已知平面内A，B，C，D这4个点中任何3个点都不在一条直线上，写出由其中每3点为顶点的所有三角形．

分析 直接根据组合的定义即可求出三角形的个数，再一一列举即可．

解答 解：平面内A，B，C，D这4个点中任何3个点都不在一条直线上，共有C43=4种，
分别为△ABC，△ABD，△ACD，△BCD．

点评 本题考查了组合数的计算公式，属于基础题．

练习册系列答案
相关题目
8．下面有三个命题：
①当x＞0时，2x+$\frac{1}{{2}^{x}}$的最小值为2；
②将函数y=cos2x的图象向右平移$\frac{π}{6}$个单位，可以得到函数y=sin（2x-$\frac{π}{6}$）的图象；
③在Rt△ABC中，AC⊥BC，AC=a，BC=b，则△ABC的外接圆半径r=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$；类比到空间，若三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直，且长度分别为a、b、c，则三棱锥S-ABC的外接球的半径R=$\frac{\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}}{2}$．
其中错误命题的序号为①②（把你认为错误命题的序号都填上）
9．若将函数f（x）=sin2x+cos2x的图象向右平移φ（φ＞0）个单位，所得图象关于原点对称，则φ的最小值为（　　）
A．$\frac{π}{8}$B．$\frac{π}{4}$C．$\frac{3π}{8}$D．$\frac{3π}{4}$
6．已知p：“直线l的倾斜角α=$\frac{π}{4}$”；q：“直线l的斜率k=1”，则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
13．已知10名工人某天生产同一零件，生产件数的茎叶图如图所示，则众数为14．
3．某几何体的三视图如图所示，则该几何体的外接球的体积为（　　）
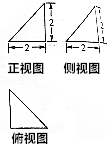
A．12πB．4$\sqrt{3}$πC．48πD．32$\sqrt{3}π$
10．已知100件产品中有4件次品，无放回地从中抽取2次，每次抽取1件，求下列事件的概率：
（1）第一次取到次品，第二次取到正品；
（2）两次都取到正品；
（3）两次抽取中恰有一次取到正品．
7．△ABC为边长为6的正三角形，则$\overrightarrow{AB}$$•\overrightarrow{AC}$=18．
19．已知角θ的顶点在平面直角坐标系xOy原点O，始边为x轴正半轴，终边在直线x-2y=0上，则sin2θ=（　　）
A．$\frac{4}{5}$B．-$\frac{4}{5}$C．$\frac{3}{5}$D．-$\frac{3}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网