题目内容
11.已知一组数据按从小到大的顺序排列为:14,19,x,23,27,其中中位数是22,则x的值为( )| A. | 24 | B. | 23 | C. | 22 | D. | 21 |
分析 把给出的此组数据中的数按从小到大(或从大到小)的顺序排列,由于数据个数是8,8是偶数,所以处于中间的两个数的平均数就是此组数据的中位数;再根据中位数是22,说明x必须排在第四的位置;据此解答即可.
解答 解:按从小到大的顺序排列:14、19、x、23、27,
中位数是22,
所以x=22,
故选:C.
点评 本题考查了中位数的知识,根据中位数的意义和此组数据的中位数,确定出x的位置是解决此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知p:“直线l的倾斜角α=$\frac{π}{4}$”;q:“直线l的斜率k=1”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.某几何体的三视图如图所示,图中网格每个小正方形的边长都为1,则该几何体的体积等于( )


| A. | $\frac{28}{3}$π | B. | $\frac{20}{3}$π | C. | 4π | D. | $\frac{8}{3}$π |
3.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
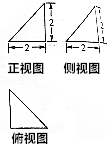

| A. | 12π | B. | 4$\sqrt{3}$π | C. | 48π | D. | 32$\sqrt{3}π$ |
20.以下各式当n→∞时,极限值为$\frac{1}{2}$的是( )
| A. | $\frac{n-2}{2n(n+1)}$ | B. | $\frac{2{n}^{2}+1}{4n+1}$ | ||
| C. | ($\sqrt{n+1}$-$\sqrt{n}$)$\sqrt{n}$ | D. | $\frac{1+4+7+…+(3n-2)}{2{n}^{2}}$ |
12.为了得到函数y=3sin$\frac{x}{3}$的图象,只需把函数y=sinx图象上所有的点的( )
| A. | 横坐标伸长到原来的3倍,纵坐标变为原来的3倍 | |
| B. | 横坐标缩小到原来的$\frac{1}{3}$倍,纵坐标变为原来的$\frac{1}{3}$倍 | |
| C. | 横坐标伸长到原来的$\frac{1}{3}$倍,纵坐标变为原来的3倍 | |
| D. | 横坐标伸长到原来的3倍,纵坐标变为原来的$\frac{1}{3}$倍 |