题目内容
12.已知函数y=f(x)在x=x0处可导,则$\underset{lim}{h→∞}\frac{f({x}_{0}+h)-f({x}_{0}-h)}{h}$等于( )| A. | f′(x0) | B. | 2f′(x0) | C. | -2f′(x0) | D. | 0 |
分析 根据导数的定义求解即可.
解答 解:∵函数y=f(x)在x=x0处可导,
$\underset{lim}{h→∞}\frac{f({x}_{0}+h)-f({x}_{0}-h)}{h}$
=$\underset{lin}{h→}2\frac{f({x}_{0}+h)-f({x}_{0}-h)}{2h}$
=2f′(x0),
故选:B.
点评 本题主要考查函数导数的概念,属于基础题.

练习册系列答案
相关题目
3.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
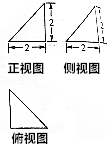

| A. | 12π | B. | 4$\sqrt{3}$π | C. | 48π | D. | 32$\sqrt{3}π$ |
20.以下各式当n→∞时,极限值为$\frac{1}{2}$的是( )
| A. | $\frac{n-2}{2n(n+1)}$ | B. | $\frac{2{n}^{2}+1}{4n+1}$ | ||
| C. | ($\sqrt{n+1}$-$\sqrt{n}$)$\sqrt{n}$ | D. | $\frac{1+4+7+…+(3n-2)}{2{n}^{2}}$ |
12.为了得到函数y=3sin$\frac{x}{3}$的图象,只需把函数y=sinx图象上所有的点的( )
| A. | 横坐标伸长到原来的3倍,纵坐标变为原来的3倍 | |
| B. | 横坐标缩小到原来的$\frac{1}{3}$倍,纵坐标变为原来的$\frac{1}{3}$倍 | |
| C. | 横坐标伸长到原来的$\frac{1}{3}$倍,纵坐标变为原来的3倍 | |
| D. | 横坐标伸长到原来的3倍,纵坐标变为原来的$\frac{1}{3}$倍 |
13.计算:cos25°sin55°-cos65°cos55°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |